Beregner statistikken for en linje ved å bruke "minste kvadraters" metode for å beregne en rett linje som er best tilpasset dataene, og returnerer en matrise som beskriver linjen. Ettersom denne funksjonen returnerer en matrise av verdier, må den skrives inn som en matriseformel.
Formelen for linjen er:
y = mx + b eller
y = m1x1 + m2x2 + ... + b (hvis det er flere områder med x-verdier)
der den avhengige y-verdien er en funksjon av de uavhengige x-verdiene. M-verdiene er koeffisienter som svarer til hver enkelt x-verdi, og b er en konstantverdi. Legg merke til at y, x og m kan være vektorer. Matrisen som RETTLINJE returnerer, er {mn,mn-1,...,m1,b}. RETTLINJE kan også returnere flere regresjonsstatistikker.
Syntaks
RETTLINJE(kjente_y;kjente_x,konst;stats)
Kjente_y er settet med y-verdier som du allerede kjenner i forholdet y = mx + b.
-
Hvis matrisen kjente_y er i en enkelt kolonne, tolkes hver kolonne med kjente_x som en separat variabel.
-
Hvis matrisen kjente_y er i én rad, blir hver rad med kjente_x tolket som en egen variabel.
Kjente_x er et valgfritt sett med x-verdier som du eventuelt kjenner i forholdet y = mx + b.
-
Matrisen kjente_x kan omfatte ett eller flere sett med variabler. Hvis det bare er brukt ett sett med variabler, kan kjente_y og kjente_x være områder med en hvilken som helst form, så lenge de har de samme dimensjonene. Hvis flere variabler blir brukt, må kjente_y være en vektor (dvs. et område med en høyde på én rad eller en bredde på én kolonne).
-
Hvis kjente_x er utelatt, blir det satt lik matrisen {1;2;3;...} som er den samme størrelsen som kjente_y.
Konst er en logisk verdi som angir om konstanten b skal tvinges til å være lik 0 eller ikke.
-
Hvis konst er SANN eller utelates, beregnes b normalt.
-
Hvis konst er USANN, angis b til er lik 0, og m-verdiene tilpasses til y = mx.
Stats er den logiske verdien som angir om ekstra regresjonsstatistikk skal returneres.
-
Hvis stats er SANN, returnerer RETTLINJE den ekstra regresjonsstatistikken, slik at den returnerte matrisen blir {mn;mn-1,...;m1;b;sen;sen-1,...;se1;seb;r 2;sey; F;df;ssreg;ssresid}.
-
Hvis stats er USANN eller utelates, returnerer RETTLINJE bare m-koeffisientene og konstanten b.
Den ekstra regresjonsstatistikken er som følger:
| Statistikk | Beskrivelse |
|---|---|
| se1;se2,...;sen | Standard feilverdier for koeffisientene m1,m2,...,mn. |
| seb | Standard feilverdi for konstanten b (seb = #N/A når konst er USANN). |
| r2 | Determinantens koeffisient. Sammenligner beregnede og faktiske y-verdier, og områder i verdi fra 0 til 1. Hvis den er 1, blir det en perfekt korrelasjon i eksemplet Det er ingen forskjell mellom den beregnede y-verdien og den faktiske y-verdien. I den andre yttergrensen er det slik at hvis determinantens koeffisient er 0, kan ikke regresjonsligningen brukes til å forutse en y-verdi. Hvis du vil ha informasjon om hvordan r2 beregnes, se "Kommentarer" senere i dette emnet. |
| sey | Standard feilverdi for y-beregningen. |
| F | F-statistikken, eller F-observert verdi. Bruk F-statistikken til å bestemme om den observerte relasjonen mellom de avhengige og uavhengige variablene inntreffer tilfeldig. |
| df | Frihetsgrader. Bruk frihetsgradene til å hjelpe å finne F-kritiske verdier i en statistikktabell. Sammenlign verdiene du finner i tabellen, med F-statistikken som returneres av RETTLINJE, for å bestemme et tillitsnivå for modellen. Hvis du vil ha informasjon om hvordan du beregner df, se "Kommentarer" senere i dette emnet. Eksempel 4 nedenfor viser bruken av F og df. |
| ssreg | Regresjonssummen av kvadrater. |
| ssresid | Restsummen av kvadrater. Hvis du vil ha informasjon om hvordan ssreg og ssresid beregnes, se "Kommentarer" senere i dette emnet. |
Følgende illustrasjon viser i hvilken rekkefølge den ekstra regresjonsstatistikken returneres.

Kommentarer
- Du kan beskrive alle rette linjer med stigningstallet og y-skjæringspunktet:
Stigningstall (m):
Hvis du vil finne stigningstallet for en linje, ofte skrevet som m, tar du to punkt på linjen, (x1,y1) og (x2,y2). Stigningstallet er lik (y2 - y1)/(x2 - x1).Y-skjæringspunkt (b):
Y-skjæringspunktet for en linje, ofte skrevet som b, er verdien av y ved punktet der linjen krysser y-aksen.Ligningen av en rett linje er y = mx + b. Når du kjenner verdiene av m og b, kan du beregne alle punktene på linjen ved å legge y- og x-verdien inn i ligningen. Du kan også bruke TREND-funksjonen.
- Når du bare har én uavhengig y-variabel, kan du finne verdiene for stigningstallet og y-skjæringspunktet direkte ved hjelp av følgende formler:
Stigningstall:
=INDEKS(RETTLINJE(kjente_y,kjente_x),1)Y-skjæringspunkt:
=INDEKS(RETTLINJE(kjente_y,kjente_x),2) - Nøyaktigheten av linjen som beregnes av RETTLINJE, avhenger av graden av punkt i dataene. Jo mer lineære dataene er, jo mer nøyaktig blir RETTLINJE-modellen. RETTLINJE bruker de minste kvadraters metode for å bestemme beste tilpassing av dataene. Når du bare har én uavhengig x-variabel, baseres beregningene for m og b på følgende formler:
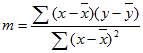
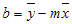
der x og y er utvalgsgjennomsnitt, for eksempel x = GJENNOMSNITT(kjente_x) og y = GJENNOMSNITT(kjente_y).
- Funksjonene RETTLINJE og KURVE beregner henholdsvis den rette linjen og den eksponentielle kurven som passer best til dataene. Du må imidlertid selv avgjøre hvilket av de to resultatene som passer best til dataene. Du kan beregne TREND(kjente_y,kjente_x) for en rett linje, eller VEKST(kjente_y, kjente_x) for en eksponentiell kurve. Disse funksjonene, uten argumentet nye_ x, returnerer en matrise med y-verdier som forutses langs linjen eller kurven ved dine faktiske datapunkt. Du kan deretter sammenligne de anslåtte verdiene med de faktiske verdiene. Det er enklere å se forskjellene mellom verdiene dersom du fremstiller dem grafisk i et diagram.
- I regresjonsanalyser beregner Microsoft Excel den kvadrerte differansen mellom den anslåtte og den faktiske y-verdien for hvert punkt. Summen av disse kvadrerte differansene kalles kvadrert residualsum, ssresid. Microsoft Excel beregner deretter den totale summen kvadratene, sstotal. Når konst = SANN eller utelatt, er den totale summen lik suymmen av de kvadrerte differansene mellom de faktiske y-verdiene og gjennomsnittet av y-verdiene. Når konst = USANN, er den totale summen lik summen av kvadratene for de faktiske y-verdiene (uten fratrekk av den gjennomsnittlige y-verdien fra hver enkelt individuelle y-verdi). Deretter kan regresjonssummen for kvadratene, ssreg, bli funnet fra: ssreg = sstotal - ssresid. Jo lavere den kvadrerte residualsummen for kvadrater er sammenlignet med kvadrert totalsum, jo større er verdien av determinantens koeffisient, r2, som er en indikator på hvor godt ligningen fra regresjonsanalysen forklarer forholdet mellom variablene. r2 er lik ssreg/sstotal.
- Noen ganger kan det hende at én eller flere av X kolonnene (anta at Y and X er i kolonner) ikke har ekstra forutsett verdi hvis det finnes andre X-kolonner. Med andre ord: Ved å eliminerere én eller flere X-kolonner, kan det føre til forutsette Y-verdier som er like nøyaktige. I dette tilfellet bør disse overflødige X-kolonnene utelates fra regresjonsmodellen. Dette fenomenet kalles “kolinearitet” fordi enhver overflødig X-kolonne kan uttrykkes som en sum av intervaller av nødvendige X-kolonner. RETTLINJE kontrollerer om det finnes kolinearitet og fjerner overflødige X-kolonner fra regresjonsmodellen når de identifiseres. X-kolonner som er blitt fjernet, kan gjenkjennes i utdata for RETTLINJE ved å ha både 0 koeffisienter og 0 se. Hvis én eller flere kolonner er fjernet som overflødige, påvirkes df fordi df er avhengig av antallet X-kolonner som faktisk er brukt til forutseende formål. Hvis du vil se beregningen av df mer detaljert, se eksempel 4 nedenfor. Hvis df er endret fordi overflødige X-kolonner er blitt fjernet, er også verdier av sey and F påvirket. Kolinearitet bør være relativ sjeldent i praksis. Det er imidlertid ett tilfelle der det kan dukke opp, og det er når noen X-kolonner bare inneholder 0 og 1 som indikatorer på om et emne i et eksperiment regnes som medlem av en bestemt gruppe eller ikke. Hvis konst er SANN eller utelatt, setter RETTLINJE effektivt inn en ekstra X-kolonne på alle 1 for å vise skjæringspunktet. Hvis du har en kolonne med 1 for hvert emne hvis det er hannkjønn eller 0 hvis ikke, og du også har en kolonne med 1 for hvert emne hvis det er hunnkjønn eller 0 hvis ikke, er den sistnevnte kolonnen overflødig fordi oppføringer i den kan hentes ved å trekke oppføringen i kolonnen “hannkjønn indikator” fra oppføringen i den ekstra kolonnen på alle 1 som er lagt til av RETTLINJE.
- df beregnes som vist når ingen X-kolonner er fjernet fra modellen på grunn av kolinearitet. Hvis det finnes k-kolonner med kjente_x og konst er SANN eller utelatt, er df = n – k – 1. Hvis konst er USANN , er df = n - k. I begge tilfeller er hver X-kolonne fjernet fordi kolineariteten øker df med 1.
- Formler som returnerer matriser, må angis som matriseformler.
- Når du skriver inn en matrisekonstant, for eksempel kjent_x, som et argument, må du bruke komma for å skille verdier i samme rad, og semikolon for å skille rader. Skilletegn kan være forskjellige avhengig av de lokale innstillingene i Regionale innstillinger i Kontrollpanelet.
- Du bør være oppmerksom på at y-verdiene som regresjonsligningen anslår, ikke nødvendigvis er gyldige dersom de er utenfor området for de y-verdiene du brukte til å sette opp ligningen.
Eksempel 1 Stigningstall og Y-skjæringspunkt
Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.
- Opprett en tom arbeidsbok eller et tomt regneark.
- Velg eksemplet i hjelpeemnet. Ikke merk rad- eller kolonneoverskriftene.
Velge et eksempel fra Hjelp
- Trykk CTRL+C.
- I regnearket merker du celle A1, og trykker CTRL+V.
- Hvis du vil veksle mellom å vise resultatene og vise formlene som returnerer resultatene, trykker du CTRL+` (grav aksent), eller velg Formelrevisjon på Verktøy-menyen, og velger deretter Formelrevisjonsmodus.
|
|
Obs! Formelen i eksemplet må angis som en matriseformel. Når du har kopiert eksemplet til et tomt regneark, merker du området A7:B7 med start i formelcellen. Trykk F2, og trykk deretter CTRL+SKIFT+ENTER. Hvis formelen ikke er angitt som en matriseformel, er enkeltresultatet 2.
Når den legges inn som matrise, returneres stigningstall (2) og skjæringspunkt mot Y-aksen (1).
Eksempel 2 Enkel lineær regresjon
Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.
- Opprett en tom arbeidsbok eller et tomt regneark.
- Velg eksemplet i hjelpeemnet. Ikke merk rad- eller kolonneoverskriftene.

Velge et eksempel fra Hjelp
- Trykk CTRL+C.
- I regnearket merker du celle A1, og trykker CTRL+V.
- Hvis du vil veksle mellom å vise resultatene og vise formlene som returnerer resultatene, trykker du CTRL+` (grav aksent), eller velg Formelrevisjon på Verktøy-menyen, og velger deretter Formelrevisjonsmodus.
|
|
Vanligvis er SUMMER({m,b}*{x,1}) lik mx + b, den beregnede y-verdien for en gitt x-verdi. Du kan også bruke TREND-funksjonen.
Eksempel 3 Flerlineær regresjon
Anta at en byggmester vurderer å kjøpe å gruppe bygninger beregnet for småbedrifter i et etablert forretningsområde.
Byggmesteren kan bruke flerlineær regresjonsanalyse til å beregne verdien av et kontorbygg i et gitt område basert på følgende variabler.
| Variabel | Refererer til |
|---|---|
| y | Taksert verdi på kontorbygget |
| x1 | Gulvareal i kvadratmeter |
| x2 | Antall kontorer |
| x3 | Antall innganger |
| x4 | Alder på kontorbygget |
I dette eksemplet forutsettes det at det eksisterer en rettlinjet relasjon mellom hver uavhengige variabel (x1, x2, x3 og x4) og den avhengige variabelen (y), verdien på kontorbygg i området.
Byggmesteren velger et tilfeldig utvalg på 11 kontorbygg av 1 500 alternativer, og henter følgende data. "Halv inngang" betyr leveringsinngang for varer.
Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.
- Opprett en tom arbeidsbok eller et tomt regneark.
- Velg eksemplet i hjelpeemnet. Ikke merk rad- eller kolonneoverskriftene.

Velge et eksempel fra Hjelp
- Trykk CTRL+C.
- I regnearket merker du celle A1, og trykker CTRL+V.
- Hvis du vil veksle mellom å vise resultatene og vise formlene som returnerer resultatene, trykker du CTRL+` (grav aksent), eller velg Formelrevisjon på Verktøy-menyen, og velger deretter Formelrevisjonsmodus.
|
|
Obs! Formelen i eksemplet må angis som en matriseformel. Når du har kopiert eksemplet til et tomt regneark, merker du området A14:E18 med start i formelcellen. Trykk F2, og trykk deretter CTRL+SKIFT+ENTER. Hvis formelen ikke er angitt som en matriseformel, er enkeltresultatet -234,2371645.
Når angitt som en matrise, returneres regresjonsstatistikken nedenfor. Bruk denne nøkkelen til å identifisere statistikken du vil ha.

Ligningen for sammensatt regresjon y = m1*x1 + m2*x2 + m3*x3 + m4*x4 + b kan nå hentes ved hjelp av verdiene fra 14:
y = 27,64*x1 + 12 530*x2 + 2 553*x3 - 234,24*x4 + 52 318
Byggmesteren kan nå beregne den takserte verdien av et kontorbygg i det samme området som er på 2 500 kvadratmeter, har tre kontorer og to innganger, og som er 25 år gammelt, ved hjelp av følgende ligning:
y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318 = kr 158,261
Eller du kan kopiere følgende tabell til celle A21 i eksempelarbeidsboken.
| Gulvareal (x1) | Kontorer (x2) | Innganger (x3) | Alder (x4) | Taksert verdi (y) |
|---|---|---|---|---|
| 25 000 | 3 | 2 | 25 | =D14*A22 + C14*B22 + B14*C22 + A14*D22 + E14 |
Du kan også bruke TREND-funksjonen til å beregne denne verdien.
Eksempel 4 Bruke F- og R2-statistikken
I det forrige eksemplet hadde determinantens koeffisient, eller r2, verdien 0,99675 (se celle A17 i utdataene for RETTLINJE), som indikerer en sterk relasjon mellom de uavhengige variablene og salgsprisen. Du kan bruke F-statistikken til å bestemme om disse resultatene, med en så høy r2-verdi, har oppstått ved en tilfeldighet.
Tenk deg at det for øyeblikket ikke er noen relasjon mellom variablene, men at du har valgt et sjeldent utvalg av 11 kontorbygg som forårsaker at statistikkanalysen viser en sterk relasjon. Begrepet "Alfa" brukes for sannsynligheten for at det feilaktig konkluderes at det finnes en relasjon.
F og df i utdata for RETTLINJE kan brukes til å anslå sannsynligheten av en høyere F-verdi som har oppstått ved en tilfeldighet. F kan sammenlignes med de kritiske verdiene i publiserte F-fordelingstabeller, eller FDIST i Excel kan brukes til å beregne sannsynligheten for en større F-verdi som oppstår ved en tilfeldighet. Den passende F-fordeling har frihetsgradene v1 og v2. Hvis n er antall datapunkt og konst er SANN eller utelatt, er v1 = n – df – 1 and v2 = df. (Hvis konst er USANN, da er v1 = n – df og v2 = df.) FDIST i Excel (F,v1,v2) returnerer sannsynligheten for en høyere F-verdi som oppstår ved en tilfeldighet. I eksempel 4 er df = 6 (celle B18) og F = 459.753674 (celle A18).
Forutsatt at en Alfa-verdi er 0,05, v1 = 11 – 6 – 1 = 4 og v2 = 6, er det kritiske nivået for F 4,53. Siden F = 459,753674 er mye høyere enn 4,53, er det ekstremt usannsynlig at en så høy F-verdi oppstod ved en tilfeldighet. (Med Alfa = 0,05 bør hypotesen om at det ikke er noe forhold mellom kjente_y og kjente_x forkastes når F overskrider det kritiske nivået, 4,53.) Ved å bruke FDIST i Excel kan du få frem sannsynligheten for at en så høy F-verdi oppstod ved en tilfeldighet. FDIST(459,753674, 4, 6) = 1,37E-7, ekstremt lite sannsynlig. Du kan konkludere med å finne det kritiske nivået for F i en tabell, eller (ved å bruke FDIST i Excel) med at regresjonsligningen er nyttig til å anslå den takserte verdien av kontorbygg i dette området. Husk at det er kritisk å bruke riktige verdier for v1 og v2, som ble beregnet i forrige avsnitt.
Eksempel 5 Beregne T-statistikken
En annen hypotesetest vil avgjøre om hver stigningstallskoeffisient kan brukes ved beregningen av den takserte verdien av et kontorbygg i eksempel 3. Hvis du for eksempel vil kontrollere den statistiske betydningen av alderskoeffisienten, dividerer du -234,24 (stigningstallskoeffisient for alder) på 13,268 (den beregnede standardfeilen for alderskoeffisienter i celle A15). Den t-observerte verdien er:
t = m4 ÷ se4 = -234.24 ÷ 13,268 = -17,7
Hvis absoluttverdien for t høy nok, kan det konkluderes med at stigningstallskoeffisienten kan brukes ved beregningen av den takserte verdien av et kontorbygg i eksempel 3. Tabellen nedenfor viser absoluttverdiene for de t-observerte verdiene.
Hvis du slår opp i en tabell i en statistikkhåndbok, vil du se at t-kritisk, tosidig, med 6 frihetsgrader og Alfa = 0,05 er 2,447. Denne kritiske verdien kan også finnes ved å bruke TINV-funksjonen i Excel TINV(0.05,6) = 2,447. Fordi den absolutte verdien av t, 17,7, er større enn 2,447, er alder en viktig variabel ved beregning av den takserte verdien av et kontorbygg. Hver av de andre uavhengige variablene kan kontrolleres mht statistisk signifikans på lignende måte. Nedenfor følger t-observerte verdier for hver av de uavhengige variablene.
| Variabel | t-observert verdi |
|---|---|
| Gulvareal | 5,1 |
| Antall kontorer | 31,3 |
| Antall innganger | 4,8 |
| Alder | 17,7 |
Disse verdiene har alle en absoluttverdi over 2,447, og derfor kan alle variablene i regresjonsligningen brukes til å forutse den beregnede verdien på kontorbygg i området.<SPAN FPRev
 Hvordan?
Hvordan?