KONFIDENS

Se også

Returnerer en verdi som du kan bruke til å konstruere konfidensintervallet til gjennomsnittet for en populasjon. Konfidensintervallet er et verdiområde. Utvalgsgjennomsnittet, x, er i midten av dette området, og området er x ± KONFIDENS. Hvis for eksempel x er utvalgsgjennomsnittet for leveringstider for produkter bestilt gjennom posten, er x ± KONFIDENS et gjennomsnittsområde for populasjon. For alle gjennomsnitt for populasjon, μ₀, i dette området er sannsynligheten for å få et utvalgsgjennomsnitt lenger fra μ₀ enn x , større enn alfa. For alle gjennomsnitt for populasjon, μ₀, som ikke er i dette området, er sannsynligheten for å få et utvalgsgjennomsnitt lenger fra μ₀ enn x , mindre enn alfa. Det vil si, anta at vi bruker x, standardavvik og størrelse for å konstruere en tosidig test ved alfa signifikansnivå fra hypotesen om at gjennomsnittet for populasjonen er μ₀. Da vil vi ikke forkaste hypotesen hvis μ₀ er i konfidensintervallet, men vil forkaste hypotesen hvis μ₀ ikke er i konfidensintervallet. Konfidensintervallet lar oss ikke slutte at det er sannsynlighet 1 - alpha for at vår neste pakke vil ha en leveringstid som er i konfidensintervallet.

Syntaks

KONFIDENS(alfa;standardavvik;størrelse)

Alfa    er signifikansnivået som brukes til å beregne konfidensnivået. Konfidensnivået er lik 100*(1 - alfa) %, eller med andre ord, en alfa på 0,05 angir et konfidensnivå på 95 %.

Standardavvik    er populasjonens standardavvik for dataområdet og antas å være kjent.

Størrelse    er størrelsen på utvalget.

Kommentarer

• Hvis et av argumentene er ikke-numerisk, returnerer KONFIDENS feilverdien #VERDI!.
• Hvis alfa ≤ 0 eller alfa ≥ 1, returnerer KONFIDENS feilverdien #NUM!.
• Hvis standardavvik ≤ 0, returnerer KONFIDENS feilverdien #NUM!.
• Hvis størrelse ikke er et heltall, avkortes det.
• Hvis størrelse < 1, returnerer KONFIDENS feilverdien #NUM!.
• Hvis vi antar at alfa er lik 0,05, må vi beregne området under standard normalkurven som er lik (1 - alfa), eller 95 %. Denne verdien er ± 1,96. Konfidensintervallet blir derfor:

  

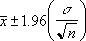
Eksempel

Sett at i et materiale på 50 pendlere er gjennomsnittlig reisetid til arbeidet 30 minutter, med et standardavvik for populasjonen på 2,5. Med alfa = .05, KONFIDENS(.05, 2.5, 50) returnerer 0,69291. Det tilsvarende konfidensintervallet er da 30 ± 0,69291 = tilnærmet [29,3, 30,7]. For alle gjennomsnitt for populasjon, μ₀, i dette intervallet er sannsynligheten for å få et utvalgsgjennomsnitt lenger fra μ₀ enn 30, mer enn 0,05. Likeledes, for alle gjennomsnitt for populasjon, μ₀, utenfor dette intervallet er sannsynligheten for å få et utvalgsgjennomsnitt lenger fra μ₀ enn 30, mindre enn 0,05.

Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.

Hvordan?