Returns the normal distribution for the specified mean and standard deviation. This function has a very wide range of applications in statistics, including hypothesis testing.
Syntax
NORMDIST(x,mean,standard_dev,cumulative)
X is the value for which you want the distribution.
Mean is the arithmetic mean of the distribution.
Standard_dev is the standard deviation of the distribution.
Cumulative is a logical value that determines the form of the function. If cumulative is TRUE, NORMDIST returns the cumulative distribution function; if FALSE, it returns the probability mass function.
Remarks
- If mean or standard_dev is nonnumeric, NORMDIST returns the #VALUE! error value.
- If standard_dev ≤ 0, NORMDIST returns the #NUM! error value.
- If mean = 0, standard_dev = 1, and cumulative = TRUE, NORMDIST returns the standard normal distribution, NORMSDIST.
- The equation for the normal density function (cumulative = FALSE) is:
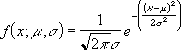
-
When cumulative = TRUE, the formula is the integral from negative infinity to x of the given formula.
Example
The example may be easier to understand if you copy it to a blank worksheet.
- Create a blank workbook or worksheet.
- Select the example in the Help topic. Do not select the row or column headers.
Selecting an example from Help
- Press CTRL+C.
- In the worksheet, select cell A1, and press CTRL+V.
- To switch between viewing the results and viewing the formulas that return the results, press CTRL+` (grave accent), or on the Tools menu, point to Formula Auditing, and then click Formula Auditing Mode.
|
|
 How?
How?