INTERCEPT

See Also

Calculates the point at which a line will intersect the y-axis by using existing x-values and y-values. The intercept point is based on a best-fit regression line plotted through the known x-values and known y-values. Use the INTERCEPT function when you want to determine the value of the dependent variable when the independent variable is 0 (zero). For example, you can use the INTERCEPT function to predict a metal's electrical resistance at 0°C when your data points were taken at room temperature and higher.

Syntax

INTERCEPT(known_y's,known_x's)

Known_y's    is the dependent set of observations or data.

Known_x's    is the independent set of observations or data.

Remarks

• The arguments should be either numbers or names, arrays, or references that contain numbers.
• If an array or reference argument contains text, logical values, or empty cells, those values are ignored; however, cells with the value zero are included.
• If known_y's and known_x's contain a different number of data points or contain no data points, INTERCEPT returns the #N/A error value.
• The equation for the intercept of the regression line, a, is:

  

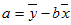
  where the slope, b, is calculated as:

  

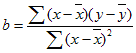
  and where x and y are the sample means AVERAGE(known_x's) and AVERAGE(known_y's).

Example

The example may be easier to understand if you copy it to a blank worksheet.

How?