Use Automatic Drift Correction on Standard Intensities
Probe for EPMA uses a sophisticated automatic drift correction to correct the counts on the standard, interference and MAN standard intensities. This standard drift correction should not be confused with the beam drift correction described previously. With the automatic standard drift correction, when Probe for EPMA loads the unknown count data to analyze a sample data point, the program will automatically check each element to see if the standard for that channel was measured both before and after the data on the unknown. If there exist sufficient standard sets, the program will automatically compute a linear interpolated drift corrected analysis.
If there are only a single standard data set, the program will simply use the set of counts on that standard which occurred closest in time prior to the unknown. Thus it is possible to perform analyses of unknowns as they are acquired, although they will not be corrected for drift. Later, when the standards have been run again, the program can recalculate all the analyses, and they will be corrected for standard count drift in real time.
The user may go back and acquire each standard up to 20 times during a run (20 "sets" of counts on the standard) and the program will determine which two sets, if any, were made closest, before and after, the counts on the unknown. The form of the standard drift correction is shown below :
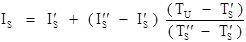
Where
:
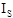is the drift corrected standard intensity
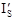is the standard intensity from the preceding standardization
is the
standard intensity from the following standardization
is the
real time of the unknown analysis
is the
real time of the preceding standardization
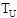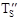is the
real time of the following standardization
The following explanation will demonstrate how the standard drift correction is actually implemented in Probe for EPMA. The example data shown here consists of four standard data points (set 1), followed by three unknown data points (points 5, 6 and 7), followed by four more standard data points (set 2), followed by three more unknown data points (points 12, 13, and 14), followed by a final four standard data points (set 3).
The first graph shows the standard intensities and how they are applied to unknown data without the use of a standard drift correction. The stepped horizontal lines drawn between the standard sets represents the standardization intensities that the program would calculate in the absence of a drift correction. In other words, the standard intensity is always based on the last standardization and remains constant until the next standardization.
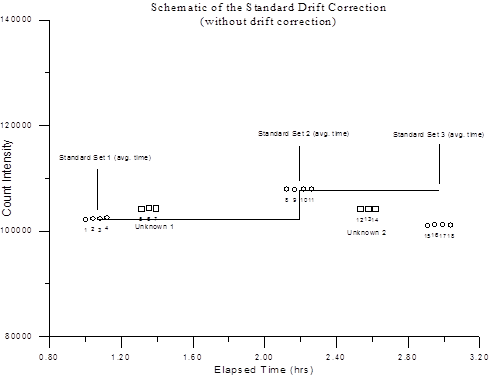
Note that each unknown data point actually uses the average intensity of the previous standardization. In a situation where drift has occurred, significant errors will result for the unknown analyses without a drift correction for the standard intensity.
The second graph shows the standard intensities and how they are applied to unknown data with the use of a standard drift correction. The sloped horizontal lines drawn between the standard sets represents the standardization intensities that the program will calculate when a standard drift correction is used. Note that each unknown data point uses the interpolated average intensity of the previous and the subsequent standardizations. In a situation where linear drift has occurred, the standard drift correction allows for the adjustment of standard intensities for intervening unknown analyses.
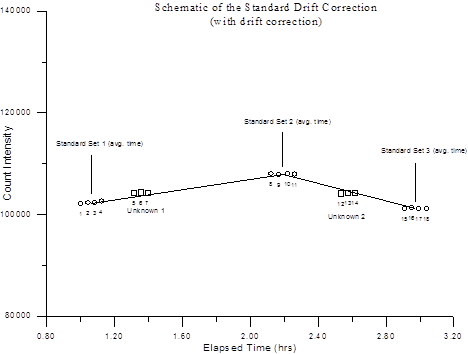
Note that because all quantitative samples (standard and unknowns) are treated as unknowns for the purposes of quantitative analysis, the standard drift correction is also applied to the analysis of standard samples. However, it is useful to note that for a given primary (assigned) standard sample, standard data points acquired just before the average time of acquisition of that standard are interpolated between the previous standard and the standard itself, while standard data points acquired just after the average time of acquisition of that standard are interpolated between the standard itself and the subsequent standard. Therefore, for primary standards, the data points within that standard are normally analyzed using two different standard intensity data sets. Furthermore, even in the case of no standard drift correction, the program will still utilize two different standard intensities when analyzing those data points just before or just after the average time of acquisition of the standard.