Use Assigned or Self Time Dependent Intensity (TDI) Corrections on Unknowns
This option will either enable or disable the Time Dependent Intensity (TDI) element corrections for subsequent quantitative analysis. This option is automatically loaded if Time Dependent Intensity (TDI) element corrections are specified by the user. Use this option to easily toggle the Time Dependent Intensity (TDI) element corrections on or off, for all quantitative analyses. Note the VOL%: line in the log window also shows the relative percent change in the intensity due to the Time Dependent Intensity (TDI) correction.
Both the assigned Time Dependent Intensity (TDI) and self Time Dependent Intensity (TDI) corrections are calculated based on the actual elapsed time of the calibration and the unknown intensity can be corrected for two different fit models:
· Use Linear Fit (slope coefficient only) for Time Dependent Intensity (TDI) Extrapolation
· Use Quadratic Fit (two coefficient) for Time Dependent Intensity (TDI) Extrapolation
The linear fit is a simple correction based on a straight line fit of the log intensities as a function of time. In other words the x data is elapsed time, the y data is the natural log of the count rate and the fit is a straight line fit in log space. The fit returned is of the y = a + bx form where b is the slope and a is the intercept. In the case of the linear fit, only the slope of the fit is applied to the unknown intensities as shown here. This is the normal correction and works well for situations where the intensity change is linearly exponential.
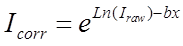
where: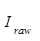 
is the uncorrected intensity
(cps)
b is the slope of the fit to the natural log intensity versus time
x is one half the total elapsed time of the measurement in seconds
The quadratic fit uses both the slope and curvature coefficients to the log intensity 2nd order polynomial fit to handle situations where the intensity change is non-linear. This non-linear intensity change can occur when the beam current is too high or the beam is too focused. In these cases where the relative percent change in intensity can exceed 100%, it is sometimes helpful to apply the quadratic fit.
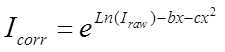
where: 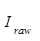is the uncorrected intensity
(cps)
b is the slope of the fit to the natural log intensity versus time
c is the curvature of the fit to the natural log intensity versus time
x is one half the total elapsed time of the measurement in seconds
It is surmised that this quadratic non-linear or hyper exponential fit is the result of two separate exponential intensity change mechanisms with different time constants that are overlapping in time.
Note that these options are disabled for current versions of the software since these options are now specified on an element by element basis in the Standard Assignments dialog from the Analyze! window.