Nyquist and Shannon's Sampling Theorems

The Nyquist theorem concerns digital sampling of a continuous time analog waveform, while Shannon’s Sampling theorem concerns the creation of a continuous time analog waveform from digital, discrete samples.

Nyquist Theorem

The Nyquist theorem states that an analog signal must be sampled at least twice as fast as the bandwidth of the signal to accurately reconstruct the waveform; otherwise, the high-frequency content creates an alias at a frequency inside the spectrum of interest (passband). An alias is a false lower frequency component that appears in sampled data acquired at too low a sampling rate. The following figure shows a 5 MHz sine wave digitized by a 6 MS/s analog-to-digital converter (ADC). In this figure, the solid line represents the sine wave being digitized, while the dotted line represents the aliased signal recorded by the ADC at that sample rate.

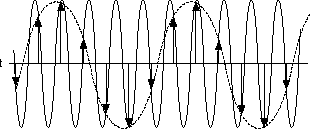
The 5 MHz frequency aliases back in the passband, falsely appearing as a 1 MHz sine wave.

Shannon’s Sampling Theorem

Shannon’s Sampling theorem states that a digital waveform must be updated at least twice as fast as the bandwidth of the signal to be accurately generated. The same image that was used for the Nyquist example can be used to demonstrate Shannon’s Sampling theorem. The following figure shows a desired 5 MHz sine wave generated by a 6 MS/s DAC. The solid line represents the desired waveform, and the arrows represent the digitized samples that are available to recreate the continuous time 5 MHz sine wave. The dotted line indicates the signal that would be seen, for example, with an oscilloscope at the output of a DAC.

In this case, the high–frequency sine wave is the desired signal, but was severely undersampled by only being generated by a 6 MS/s DAC; the actual resulting waveform is a 1 MHz signal.

In systems where you want to generate accurate signals using sampled data, the sampling rate must be set high enough to prevent aliasing.