Mathematical Method
In both cases, the slope coefficient is calculated using a linear fit of intensity versus elapsed time. In this method intensities of different magnitude can be corrected using the same slope (as opposed to using the Y-intercept). Intensities that are less than or equal to zero are ignored. The count data is normalized to counts per second and the natural log taken. The elapsed time is converted to seconds and the linear (straight line) fit is calculated from the midpoint of the elapsed time. Only the slope parameter is saved for the actual Time Dependent Intensity (TDI) correction to allow the correction to be applied to a variety of samples that may contain different absolute intensities at different times (due to beam or standard drift) although the third coefficient is utilized for the quadratic exponential Time Dependent Intensity (TDI) correction.
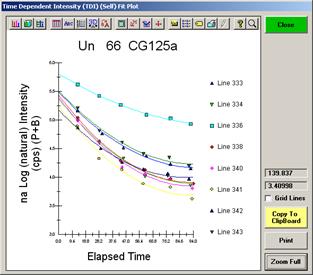
This new option allows the user to set the Time Dependent Intensity (TDI) element fit type to log-linear (exponential) or to log-quadratic (hyper-exponential) on an element by element basis. The hyper-exponential fit is useful in cases where the intensity decay is non-exponential. This is usually the case for Na loss in hydrous-alkali glasses where the intensity loss is greater than 50%.
Note that the linear TDI correction utilizes only the slope of the TDI fit in log space. However the “hyper-exponential” TDI correction utilizes the actual intercept of the 2nd order quadratic fit to the TDI data. An exception is made in the case where the TDI element is duplicated and acquired on more than one spectrometer and if it is then calculated using the “aggregate” intensity option. In this case the slope and curvature of the 2nd order quadratic is utilized for the extrapolation to zero time.
Once the slope is calculated it is used in the following expression to adjust the unknown intensity for Time Dependent Intensity (TDI) element loss (or gain):
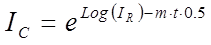
where:
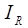 = Raw (uncorrected)
intensity in counts per second
= Raw (uncorrected)
intensity in counts per second
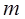 = Time
Dependent Intensity (TDI) slope coefficient from linear fit of Log intensity
versus time
= Time
Dependent Intensity (TDI) slope coefficient from linear fit of Log intensity
versus time
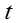 = Total
elapsed integration time
= Total
elapsed integration time
Typical Situation for Time Dependent Intensity (TDI) Correction
For instance, when sodium loss in observed in an alkali glass sample, a corresponding gain in silicon and aluminum x-rays may be noted. The extrapolation correction used in Probe for EPMA can be applied to some or all elements in an sample, regardless of whether the x-ray intensities are decreased or increased during the acquisition (as long as the elements to be corrected are acquired as the first element on each spectrometer, i.e., order number = 1).
Depending on the sample, this may or may not be a valid assumption. Under certain conditions, with very beam sensitive hydrous alkali glasses, the change in count rate may actually decrease more quickly than a simple log decay. In this case, it may be necessary to defocus the beam slightly or reduce the beam current before acquisition.
How to Use the Time Dependent Intensity (TDI) Correction
To utilize the Time Dependent Intensity (TDI) correction first decide if you require an assigned calibration curve type correction or a self-calibration curve type correction. In the self calibration correction the user simply selects the "Self-Calibration" option (see Special Options button in the Acquire! Window) and acquires the data point(s) as one would normally. In the assigned Time Dependent Intensity (TDI) correction the user first selects a sample that is similar in Time Dependent Intensity (TDI) characteristics to the sample to which the assigned calibration curve will be assigned to (it could be the actual sample itself) and then selects the "Assigned Calibration" option (see Special Options button in the Acquire! Window). The next acquisition that is started will create a calibration curve sample that can be assigned to one or more samples for the purpose of correcting Time Dependent Intensity (TDI) loss or grow-in.
Note that if the Aggregate Intensity Analysis Option is selected and an element is also using the TDI correction, the slope correction will be applied from that determined by the first channel of the aggregate intensity element.
Self-Calibration vs Assigned Calibration
The difference between the two methods is that the assigned calibration curve will apply the same slope correction to all points within the assigned sample. Therefore the variation seen in the (assigned calibration) corrected sample concentrations reflects only the actual variation in the sample. On the other hand, the self calibration method acquires a calibration curve separately for each data point and therefore the variation from point to point may be partially due to statistical variation between the self-calibration curves.
Both of the calibration corrections are quantitative in that the correction is based on a calibration curve acquired during the run, on the sample itself or another sample of similar characteristics, and is applied during the ZAF or Phi-Rho-Z iteration phase of the analysis to correct for changes in the matrix correction due to the extrapolation correction. Any number of calibration samples may be acquired and any sample or range of samples can be assigned to use any of the calibration samples for the extrapolation correction. Note that the a previously assigned Time Dependent Intensity (TDI) element correction is automatically loaded for new unknown samples.
Note that the correction uses the actual elapsed time for all calculations to produce the best quantitative results. Nevertheless, the user should be aware that the technique must be applied carefully to obtain the best results.
Time Dependent Intensity Corrections for Standards
There are two options for acquiring standard counts, if you
intend to utilize the TDI procedure for your unknowns. One is to use the normal
counting interval on a robust standard where the elements (e.g. Na, K, Al, Si)
do not change with time under the beam. However, this might introduce some
error, as it introduces conditions different from those used for the unknown. A
second and potentially more correct approach would be to use a standard similar
to the unknown (e.g. a glass standard, if that is what the unknown is) and
acquire counts on it using the TDI method.
Time Dependent Intensity Corrections and Acquisition Order
Another concern is with samples that contain more than one
affected element on a given spectrometer. Probe for EPMA only applies the Time
Dependent Intensity (TDI) element correction for elements that are acquired
first on a given spectrometer. A user may wish to run some tests on the second
element on the spectrometer, comparing the counts to those acquired if it were
the first element, and calculate a correction factor, which could be entered in
the "specified APF" field for the element. This would be valid only to the
extent that the correction were applied to unknown samples behaving the same as
the one the test was performed on.