Quantal Analysis of Transmitter Release > Introduction
The quantal analysis module can be used to estimate the quantal content of neuromuscular nerve-evoked endplate currents or potentials, and other forms of synaptic signal, using the either the direct method, variance method, and method of failures. In circumstances where both evoked and spontaneous miniature events are available, transmitter release parameters, n, (number of available quanta) and p, probability of release, is calculated using binomial analysis.
Quantal content (direct method)
If the data file contains both evoked and miniature signals, the direct method of calculating quantal content can be used.
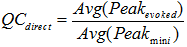 1
1
This is the most accurate method for calculating quantal content.
Quantal content (variance method)
It is not always possible to record the miniature synaptic signals, which represent single quanta. In such circumstances, it may still be possible to calculate quantal content from the variability of the evoked signal
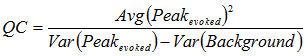 2
2
This method is dependent upon the assumption that the number of quanta released follows a Poisson distribution. This will only be the case when the probability of release is very low (i.e. p < 0.1). Since large errors can result if this condition is not satisfied, results using the variance method should be treated with caution.
Quantal Content (failures method)
If the quantal release probability is very low, a nerve stimulus may occasionally release no quanta at all, resulting in intermittent failures to evoked post-synaptic signals. Again using the assumption of a Poisson distribution controlling release, the quantal content can be calculated from
 3
3
Binomial analysis
The transmitter release process can often be modelled as a pool of n quanta available for release, with each quantum having a probability, p, of being released when the nerve is stimulated. If both evoked and spontaneous signals are available, it is possible to calculate estimates for n and p, on the assumption that the number of quanta released per stimulus follows a binomial distribution.
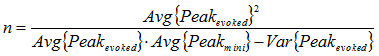 4
4
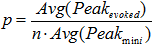 5
5
Correction for non-linear summation of potentials
Unlike currents recorded under voltage-clamp conditions, synaptic potentials do not summate linearly. Therefore the size of the synaptic potential is not directly proportional to the number of quanta released. However, given certain assumptions, it is possible to correct for the effects of non-linear summation using the eqn.
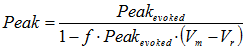 6
6
where Peakevoked is the measured peak amplitude of the evoked synaptic potential, Vm is the cell resting potential, Vr is the reversal potential for the post-synaptic ion channels, and f is a correction factor for the effects of the cell membrane time constant on synaptic potential amplitude. (A discussion on non-linear summation and its correction can be found in McLachlan & Martin, 1981).