Impedance

Impedance

Capacitive and inductive loads oppose the flow of alternating currents. This opposition is expressed as impedance at a given frequency. The effect of a real-world impedance load is observed as an attenuation of the signal and a phase shift. Because of the nature of the impedance, it is denoted as a vector whose angle is the same as the phase angle between voltage and current, and the magnitude of the impedance is the same as the quotient between the voltage and current magnitudes, as follows:

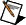Note  Bold values denote vector quantities or complex numbers.

Z = V/I

Numerically, the impedance vector is represented as a complex number either in polar form (magnitude and phase) or rectangular form (real and imaginary). The following equation expresses impedance in rectangular form:

Z = R + jX

where R and X are resistance and reactance, respectively. When X = 0, the load is purely resistive; when R = 0, the load is purely reactive. For capacitors, the reactance can be expressed as follows:

X_c = –1/(2fC_s)

For inductors, the reactance can be expressed as follows:

X_L = 2fL_s