MT Reed Solomon Symbol Encode VI

Generates a normal or shortened Reed-Solomon (RS) encoded integer symbol stream.

Reed-Solomon codes are specialized Bose-Chaudhari-Hocquenghem (BCH) codes in which the code elements are drawn from the Galois field, GF(2^m). Reed-Solomon codes are extremely powerful at burst error correction. The operations involved in Reed-Solomon encoding and decoding are performed in the GF(2^m), meaning that the Reed-Solomon encoder operates on code words that are symbols/groups of bits. As such, the input parameters code word length (n) symbols and data word length (k) symbols are specified in terms of symbols. Each symbol represents a group of Log₂(n+1) bits.

Use the pull-down menu to select an instance of this VI.

Select an instance MT RS Symbol Encoder (normal) MT RS Symbol Encoder (shortened)

Details

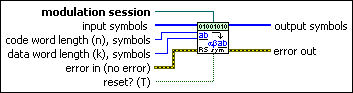
MT RS Symbol Encoder (normal)

This polymorphic instance generates a Reed-Solomon encoded integer symbol stream in normal format. The normal Reed-Solomon (n,k,t) code consists of values of n of the form n=2^m–1, where valid values of m lie in the range 2 ≤ m ≤ 16.

For example, specify n=255, k=233 to produce a Reed-Solomon (255,233,11) code. This code has an error-correcting capacity of 11 Reed-Solomon symbols.

	modulation session specifies the modulation session refnum for configuring selected attributes of the Modulation Toolkit. Use this refnum to configure the advanced attributes in the MT Reed Solomon Symbol Encode VI. Initialize the session with the MT Open Session VI. After configuring the modulation session refnum with the appropriate attributes, wire the modulation session refnum into the RS Symbol Encoder VI. If the RS Symbol Encoder VI is called with an uninitialized modulation session refnum, the VI returns an error. The default is empty.
	input symbols specifies the array of integer symbols to be encoded using the Reed-Solomon encoding scheme. Use the MT Generate Bits (poly) VI followed by MT Pack Bits VI to generate the integer symbols required for this parameter. Note  The Reed-Solomon encoder is a block encoder, meaning that it operates on a block of k integers. To ensure that the output symbols stream corresponds to the entire input symbols array, specify an input symbols stream with a length L that is an integer multiple of k symbols. If the length L is not a multiple of k symbols, the last L modulo k symbols are buffered inside the encoder. These symbols are prepended to the incoming input symbols stream at the beginning of the next iteration if reset? is set to FALSE.
	code word length (n), symbols specifies the length of the Reed-Solomon code word. Each Reed-Solomon symbol represents Log2(n+1) bits. The default is 7.
	data word length (k), symbols specifies the length of the Reed-Solomon data word. Each Reed-Solomon symbol represents Log2(n+1) bits. The default is 3.
	reset? specifies whether to clear the internal state of the Reed-Solomon encoder. By default, the VI resets on first call. When reset? is set to TRUE, the VI initializes the Galois field structure corresponding to the Reed-Solomon (n,k) values. The VI clears any buffered data from previous iterations. When reset? is set to FALSE, the VI continues performing Reed-Solomon encoding from the previous iteration. Any buffered data from the previous iteration are prepended to the input symbols stream prior to encoding. The default is TRUE.
	error in (no error) can accept error information wired from previously called VIs. Use this information to decide if any functionality should be bypassed in the event of errors from other VIs. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. code identifies the error or warning code. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. source describes the origin of the error or warning. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
	output symbols returns the Reed-Solomon encoded integer symbol stream. Wire this parameter to the MT Reed Solomon Symbol Decode VI to recover the input data stream.
	error out passes error or warning information out of a VI to be used by other VIs. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. code is the error or warning code. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. source describes the origin of the error or warning. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error.

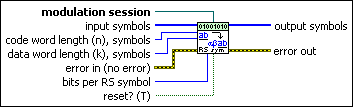
MT RS Symbol Encoder (shortened)

This polymorphic instance generates a Reed-Solomon encoded integer symbol stream in shortened format. Using shortened Reed-Solomon codes, the k and n values represent symbols. Each symbol has a length m bits, which is specified using the bits per RS symbol parameter.

Specify a shortened RS code by specifying the shortened values of n and k, as well as the bits per symbol that correspond to the underlying Galois field arithmetic. For example, you can specify code word length (n) symbols as 32, data word length (k) symbols as 28, and bits per RS symbol as 8 to generate a shortened Reed-Solomon (32,28,2) code with error-correcting capacity of two Reed-Solomon symbols. For this code, the underlying Galois field arithmetic is performed in GF(2⁸)=256.

	modulation session specifies the modulation session refnum for configuring selected attributes of the Modulation Toolkit. Use this refnum to configure the advanced attributes in the MT Reed Solomon Symbol Encode VI. Initialize the session with the MT Open Session VI. After configuring the modulation session refnum with the appropriate attributes, wire the modulation session refnum into the RS Symbol Encoder VI. If the RS Symbol Encoder VI is called with an uninitialized modulation session refnum, the VI returns an error. The default is empty.
	input symbols specifies the array of integer symbols to be encoded using the shortened Reed-Solomon encoding scheme. Use the MT Generate Bits (poly) VI followed by the MT Pack Bits VI to generate the integer symbols required for this control. The default is empty. Note   The shortened Reed-Solomon encoder is a block encoder, meaning that it operates on a block of k integers. To ensure that the output symbols stream corresponds to the entire input symbols array, specify an input symbols stream whose length L is an integer multiple of k symbols. If the length L is not a multiple of k symbols, the last L modulo k symbols are buffered inside the encoder. These symbols are prepended to the incoming input symbols stream at the beginning of the next iteration if reset? is set to FALSE.
	code word length (n), symbols specifies the length of the Reed-Solomon code word. Each Reed-Solomon symbol represents Log2(n+1) bits. The default is 7.
	data word length (k), symbols specifies the length of the Reed-Solomon data word. Each Reed-Solomon symbol represents Log2(n+1) bits. The default is 3.
	bits per RS symbol specifies the number of bits per RS symbol. This parameter specifies the Galois field over which the encoding operation is performed as GF(2bits per RS symbol). Valid values fall in the range 3–16 inclusive. For example, to specify a shortened Reed-Solomon (32,28) code in the Galois field GF(256), specify code word length (n) symbols as 32 symbols, code word length (k) symbols as 28 symbols, and bits per RS symbol as 8. The default is 3.
	reset? specifies whether to clear the internal state of the Reed-Solomon encoder. By default, the VI resets on first call. When reset? is set to TRUE, the VI initializes the Galois field structure corresponding to the Reed-Solomon (n,k) values. The VI clears any buffered data from previous iterations. When reset? is set to FALSE, the VI continues performing Reed-Solomon encoding from the previous iteration. Any buffered data from the previous iteration are prepended to the input symbols stream prior to encoding. The default is TRUE.
	error in (no error) can accept error information wired from previously called VIs. Use this information to decide if any functionality should be bypassed in the event of errors from other VIs. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. code identifies the error or warning code. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error. source describes the origin of the error or warning. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
	output symbols returns the Reed-Solomon encoded integer symbol stream. Wire this parameter to the MT Reed Solomon Symbol Decode VI to recover the input data stream.
	error out passes error or warning information out of a VI to be used by other VIs. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. code is the error or warning code. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error. source describes the origin of the error or warning. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error.

Details

The following advanced attributes can be used to configure the behavior of the Reed-Solomon Symbol Encoder and the Reed-Solomon Symbol Decoder VIs. The property node is located on the Functions palette at RF Communications»Modulation»Digital.

• RS Primitive Polynomial: Use this attribute to set the coefficients of the primitive polynomial in the underlying Galois field GF(2^m). The coefficients of the primitive polynomial must be binary valued. The Reed-Solomon Symbol Encoder VI does not check whether the input polynomial is a primitive polynomial.

  Note  If the Primitive Polynomial array is not empty, the Reed-Solomon Symbol Encoder VI uses the specified polynomial. If the Primitive Polynomial array is empty, the Reed-Solomon Symbol Encoder VI employs a lookup table of stored primitive polynomials (for GF(2m), m=2,…,16) for computing the Reed-Solomon generator polynomial.

• RS Symbol Mapping: Use this attribute to specify whether the input message and the output coded symbols are mapped to elements in the underlying Galois field GF(n+1) using the Polynomial representation or the Exponent representation.

  Polynomial(default)	This format assumes that the message symbols lie in the range [0,n], corresponding to polynomials in GF(n+1).
  Exponent	This format assumes that the input symbols represent Galois field exponents i, where i varies from –1 to n–1.

  For example, consider the specification of a (7,3) Reed-Solomon double error-correcting code. The Reed-Solomon Symbol Encoder VI can accept three Reed-Solomon message symbols (3 bits per symbol) and returns 7 Reed-Solomon encoded symbols. Assume that you input the message word [5 6 2] to the input symbols parameter of the Reed-Solomon Symbol Encoder VI. This example assumes that the RS Message Polynomial order property is set to Descending Powers of X and the RS Parity Polynomial order property is set to Descending Powers of X.

  • Case 1 — RS Symbol Mapping is set to polynomial. The Reed-Solomon encoder treats the array [5 6 2] as a polynomial m(x)=(1+ ²)x²+(+ ²)x+. The Reed-Solomon parity polynomial is computed as p(x)=x ²+ ² x+(1+) (or the array [0 1 4 3]) and returns the output encoded symbol array c(x)=x ⁴ m(x)+p(x)[0 1 4 -1 3 5 6 2].
  • Case 2 — RS Symbol Mapping is set to Exponent. The Reed-Solomon encoder treats the array [5 6 2] as a polynomial m(x)= ⁵ x ²+ ⁶ x+ ². The Reed-Solomon parity polynomial is computed as p(x)=x³+ ⁴ x ²+ ³ (or the array [0 4 –1 3] and returns the output encoded symbol array c(x)=x ⁴ m(x)+p(x)[0 4 –1 3 5 6 2].

• RS Galois primitive element: Use this property to specify the exponent q of the primitive element A= ^q in the Galois field GF(2^m). The element q determines the primitive element in the Galois field GF(2^m). Valid values of q are such that GCD (q,2m –1)=1. The default value of q equals 1. The Reed-Solomon generator polynomial is uniquely specified by the primitive polynomial (mentioned previously), the Reed-Solomon start root exponent, and the Reed-Solomon Galois primitive element.

  The Reed-Solomon generator polynomial g(x) is given as

  g(x)=(x–A^B)(x–A^B+1)(x–A^B+2)…(x–A^B+2t–1), A= ⁴

  Here B denotes the Reed-Solomon start root exponent, t denotes the error-correcting capacity of the Reed-Solomon code, and A= ⁴ denotes the Reed-Solomon Galois primitive element.

• RS Start Root Exponent (Generator polynomial): Use this property to specify the starting root exponent of the Reed-Solomon generator polynomial.

• RS Message Polynomial order, RS Parity Polynomial order: The Reed-Solomon Symbol Encoder/Decoder VIs interpret the input message stream/input coded stream as polynomials, with a format (increasing/decreasing powers of X) that is provided with attributes you set using the generic modulation session refnum. These attributes also determine the output order of the encoded symbols/recovered message symbols. The default value of both attributes is Decreasing Powers of X.

  Decreasing Powers of X(default)

  This format treats the input message polynomial in decreasing powers of x. Note   The code-word polynomial is also output in the same order. For example, consider the specification of a (7,3) Reed-Solomon double error-correcting code. The Reed-Solomon encoder inputs three Reed-Solomon message symbols (3 bits per symbol) and generates 7 Reed-Solomon encoded symbols, assuming that you enter the message word [5 6 2] to the input symbols parameter of the Reed-Solomon encoder. If RS Message Polynomial Order is set to Decreasing Powers of X, and the RS Parity Polynomial order is set to Decreasing Powers of X, the Reed-Solomon Symbol Encoder VI treats the array as a polynomial m(x)=(1+ 2)x 2+(+ 2)x+. The parity polynomial is computed to be p(x)=x 2+ 2 x+(1+) and returns the output encoded symbol array to be c(x)=x 4 m(x)+p(x) [0 1 4 3 5 6 2] (if RS Parity Position is set to Beginning) or c(x)=m(x)+x 4 p(x) [5 6 2 0 1 4 3] (if RS Parity Position is set to End).

  Increasing Powers of X

  This format treats the input message polynomial in increasing powers of x. If RS Message Polynomial Order is set to Increasing Powers of X, and RS Parity Polynomial order is set to Increasing Powers of X, the Reed-Solomon Symbol Encoder VI treats the array as a polynomial m(x)=(1+ 2)+(+ 2)x+ x 2 and returns the output encoded symbol array to be [2 5 1 6 5 6 2] (if RS Parity Position is set to Beginning) or [5 6 2 2 5 1 6] (if RS Parity Position is set to End).

• RS Shortening Zeros Location: Use this property to specify the relative position of the shortening zeros with respect to the message polynomial prior to performing Reed-Solomon encoding.

  Prior Message(default)	Places the shortening zeros before the message bits.
  Post Message	Places the shortening zeros after the message bits.

• RS Parity Position: Use this property to specify the position of the parity symbols relative to the message symbols in the Reed-Solomon code word.

  Beginning(default)	Places the parity bits at the beginning of the code word.
  End	places the parity bits at the end of the code word.

The values of (n,k) passed to the RS decoder are specified in terms of RS symbols, where n denotes the RS code word length (symbols) and k denotes the RS data word length (symbols). For decoding, choose either a normal RS code or a shortened RS code. Each normal RS-encoded symbol corresponds to Log₂(n + 1) bits. Each shortened RS-encoded symbol corresponds to the number of bits specified in the bits per RS symbol parameter.

The following table relates RS code types to data and word lengths, where L is the number of shortening zeros.

Code Type	Bits per RS Symbol (m)	Code Word Length (n)	Data Word Length (k)	Error-Correcting Capacity (t)
Reed-Solomon (normal)	Log2(n+ 1)	2m - 1	2m - 1 - 2t	(n - k)/2
Reed-Solomon (shortened)	User-specified	2m - 1 - L	2m - 1 - L - 2t	(n - k)/2