MT LDPC Decoder VI
Message-passing algorithms are effective decoding strategies for low-density parity check (LDPC). The best algorithm known is iterative probabilistic decoding, or belief propagation. In this algorithm, at each iteration, messages are passed from message nodes to check nodes and vice versa. The message that is sent from message node (v) to the check node (c) must not take into account the message sent in the previous iteration from c to v. The same is true for messages passed from check nodes to message nodes.
Use the pull-down menu to select an instance of this VI.
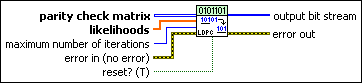
MT LDPC Decoder (Serial Schedule)
The LDPC serial decoding schedule is based on a serial update of symbol nodes messages. This update can be considered as shuffling of the flooding schedule. Instead of sending all messages from symbol nodes to check nodes and then all messages from check nodes to symbol nodes, as done in the flooding schedule, we go over the check nodes in some order and for each node we send all messages into the node and then all messages out from the node.
 |
parity check matrix specifies the parity check matrix used by the encoder for encoding. |
||||||
 |
likelihoods specifies the likelihoods of the received symbols. |
||||||
 |
maximum number of iterations specifies the maximum number of iterations for the iterative decoding process. The decoder stops iterating after number of iterations exceeds this value or if it satisfies other conditions. |
||||||
 |
reset? (T) specifies whether to clear the internal state of the decoder. By default, the VI resets on first call. |
||||||
 |
error in (no error) can accept error information wired from previously called VIs. Use this information to decide if any functionality should be bypassed in the event of errors from other VIs. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
|
||||||
 |
output bit stream returns the generated pseudorandom data bits. If the PN sequence order is N, the output data is periodic with period T = 2N–1. For example, if N = 7, the output sequence repeats after every T = 127 bits. |
||||||
 |
error out passes error or warning information out of a VI to be used by other VIs. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
|
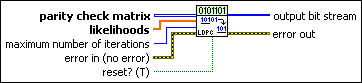
MT LDPC Decoder (Flooding Schedule)
The standard message-passing schedule for decoding LDPC code is a version of the so-called flooding schedule, in which each iteration all the symbol nodes, and subsequently all the check nodes, pass new messages to their neighbors.
 |
parity check matrix specifies the parity check matrix used by the encoder for encoding. |
||||||
 |
likelihoods specifies the likelihoods of the received symbols. |
||||||
 |
maximum number of iterations specifies the maximum number of iterations for the iterative decoding process. The decoder stops iterating after number of iterations exceeds this value or if it satisfies other conditions. |
||||||
 |
reset? (T) specifies whether to clear the internal state of the decoder. By default, the VI resets on first call. |
||||||
 |
error in (no error) can accept error information wired from previously called VIs. Use this information to decide if any functionality should be bypassed in the event of errors from other VIs. Right-click the front panel error in control and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
|
||||||
 |
output bit stream returns the generated pseudorandom data bits. If the PN sequence order is N, the output data is periodic with period T = 2N–1. For example, if N = 7, the output sequence repeats after every T = 127 bits. |
||||||
 |
error out passes error or warning information out of a VI to be used by other VIs. Right-click the front panel error out indicator and select Explain Error or Explain Warning from the shortcut menu for more information about the error.
|
Details
The decoder assumes that the parity bits are placed at the end of the code word, so it returns the first part of the code word, which are the message bits.
Belief Propagation algorithm is a sub-class of message-passing algorithms. The messages passed along the edges in this algorithm are probabilities, or beliefs. It is advantageous to work with likelihoods, or log-likelihoods instead of probabilities. For a binary random variable x, let L(x) = Pr[x = 0]/Pr[x = 1] be the likelihood of x.
Given another random variable y, the conditional likelihood of x denoted L(x / y) is defined as Pr[x =1|y] /Pr[x = 0|y].
The likelihood ratio is defined as L = Pr[x=1|y] / Pr[x=0|y]
For example, for a BSC channel, if the probability of error = p and the probability of no error = 1-p, then the likelihood ratio = (1-p)/p
It must be clear that the likelihood calculation depends upon the specific choice of the symbol map used in the modulation scheme. An example of likelihood calculation for a BPSK additive white Gaussian noise (AWGN) channel, if bit 0 is mapped to symbol point 1 and bit 1 is mapped to symbol point -1, is shown below.
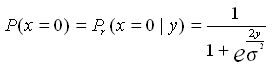
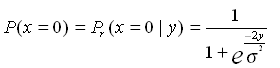
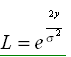
The following examples demonstrate likelihood calculations for BPSK for AWGN and BSC channels:
- MT BPSK BER vs EBN0 graph [LDPC coding]
- MT LDPC Encode Decode.vi



