Spherical Arcs

A 3D spherical arc defines a 2D circular arc in the X'Y' plane of a coordinate system that is transformed by rotation in pitch, as shown in the first figure, and yaw, as shown in the second figure, from the normal 3D coordinate space (XYZ).

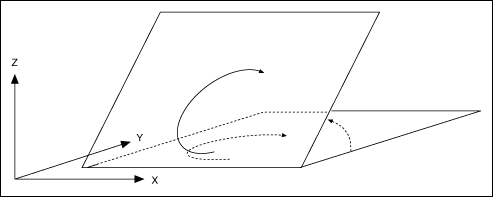
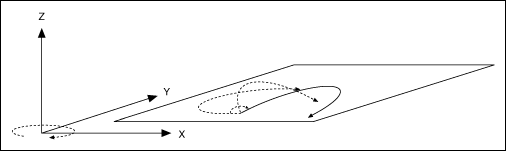
In the transformed X'Y'Z' space, the 3D arc is reduced to a simpler 2D arc. The 3D arc is defined as a 2D circular arc in the X'Y' plane of a transformed vector space X'Y'Z'. This transformed vector space, X'Y'Z', is defined in orientation only, with no absolute position offset. Its orientation is relative to the XYZ vector space, and is defined in terms of pitch and yaw angles. When rotating through the pitch angle, the Y and Y' axes stay aligned with each other while the X'Z' plane rotates around them. When rotating through the yaw angle, the Y' axis never leaves the original XY plane, as the newly-defined X'Y'Z' vector space rotates around the original Z-axis.

The radius, start angle, and travel angle parameters also apply to a spherical arc that defines the arc in two dimensions.

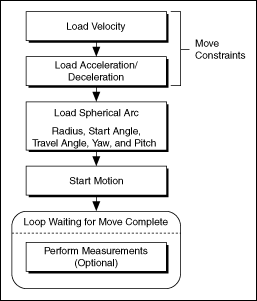
Spherical Arc Move Algorithm

The following figure shows a generic spherical arc move algorithm applicable to both C/C++ and LabVIEW code.