Validating Models (System Identification Toolkit)
Model estimation determines the best model of the system within the chosen model structure. Model estimation does not determine if the model provides the most accurate description of the system. After you obtain a model, you must validate the model to determine how well the behavior of the model corresponds to the data you measured, to any prior knowledge of the system, and to the purpose for which you use the model. Model validation also determines if the model is flexible enough to describe the system. If the model is inadequate, you must revise the system identification process or consider using another method.
 |
Note When validating the model you obtain, you must use a set of data that is different from the data you used to estimate the model. |
The best way to validate a model is to experiment with the model under real-world conditions. If the model works as you expect, the model estimation is successful. However, experimenting with the model under real-world conditions might be dangerous. For example, introducing arbitrary perturbations to the input of a chemical plant might lead to a harmful explosion. Therefore, before you incorporate the model into real-world applications, validate the model by using plots and common sense or by using statistical tests on the prediction error.
The LabVIEW System Identification Toolkit provides three of the most common validation methods—model simulation, model prediction, and model residual analysis. You can use any or all of these methods to validate the model. The method(s) you use depend on the purpose for which you created the model.
Model Simulation
Use model simulation to understand the underlying dynamic relationship between the model inputs and outputs. The SI Model Simulation VI determines the outputs of a system for given inputs. After you build a model for the system using the input and output data you measured, you can use the model to simulate the response of the system by using the model equations. You then can evaluate the behavior of the system. You also can use simulation to validate the model by comparing the simulated response with the measured response.
Refer to the Model Simulation VI in the labview\examples\System Identification\Getting Started\General.llb for an example that demonstrates how to simulate the response of an unknown system with the estimated model.
 Open example
Open example
 Browse related examples
Browse related examples
Model Prediction
Use model prediction to test the ability of the model to predict the response of the system using past input and output data. The SI Model Prediction VI determines the response of a system at time t based on the output information available at time t – k and all the inputs applied from time t – k to time t. k represents the size of the prediction window. Therefore, model prediction can determine how useful a model is in estimating future responses of the system, given all information at time t and an expected input profile in the future. Some control techniques take advantage of model prediction to improve control performance. For example, model predictive control uses some of the prediction properties of a model to determine if a particular limitation or constraint is active in the future. This method allows the controller to take preventive actions before such constraints become active.
If you have the measured input and output of a system, you also can validate the model of the system by comparing the predicted output and the measured output. If the prediction error is small, the model is acceptable.
Refer to the Model Prediction VI in the labview\examples\System Identification\Getting Started\General.llb for an example that demonstrates how to use the k-step ahead prediction to verify the model for an unknown system.
 Open example
Open example
 Browse related examples
Browse related examples
Model Residual Analysis
Use model residual analysis to analyze the prediction error, which is the difference between the response that an estimated model predicts and the actual response from the system. The following equation defines the prediction error, also known as the residual e(k).
e(k) = y(k) – y'(k)
y(k) is the measured output and y'( k) is the output from the one-step-ahead prediction. If the model is capable of describing the plant, the residual is zero-mean white noise and independent of the input signal. You can use autocorrelation analysis to test if the residual is zero-mean white noise. You can use cross-correlation analysis to test if the residual is independent of the input signal. The SI Model Residual Analysis VI calculates both the autocorrelation and the cross-correlation values.
Autocorrelation
The following equation defines the autocorrelation of the residuals.
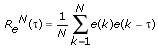
Ideally, the residual is white noise, and therefore the autocorrelation function ReN(τ) is zero when τ is nonzero. A large autocorrelation when τ is nonzero indicates that the residual is not zero-mean white noise and also implies that the model structure is not relevant to the system or that you might need to increase the model order.
In real-world applications, the autocorrelation function ReN(τ) cannot be zero when τ is nonzero because of the limited length of data points. However, the SI Model Residual Analysis VI assesses if the autocorrelation value is sufficiently small to be ignored. If the value of autocorrelation falls within the confidence range, the autocorrelation value is insignificant and you can consider this value to be equal to zero.
Cross Correlation
The following equation defines the cross correlation between residuals and past inputs.
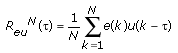
If the residual is independent of the input, the cross correlation is zero for all τ. If the residual correlates with the input, the cross correlation is nonzero, suggesting that the model did not capture all deterministic variations from the data. Therefore, you must revise the model variation.
The SI Model Residual Analysis VI assesses if the value of cross correlation is sufficiently small. If the value of cross correlation falls within the confidence range, the value is insignificant and you can consider this value to be equal to zero.
Refer to the Residual Analysis VI in the labview\examples\System Identification\Getting Started\General.llb for an example that demonstrates how to analyze the residuals of the model estimation for an unknown system.