ARMAX Model Definitions (System Identification Toolkit)
When D(z) and F(z) equal 1, the general-linear polynomial model reduces to an autoregressive-moving average with exogenous terms (ARMAX) model. Unlike the autoregressive with exogenous terms (ARX) model, the system structure of an ARMAX model includes the stochastic dynamics. ARMAX models are useful when you have dominating disturbances that enter early in the process, such as at the input. For example, a wind gust affecting an aircraft is a dominating disturbance early in the process. The ARMAX model has more flexibility than the ARX model in handling models that contain disturbances.
Use the SI Estimate ARMAX Model VI to estimate ARMAX models. This VI uses the Gauss-Newton method to optimize the mean square value of the prediction error when searching for the optimal ARMAX model. This searching process is iterative and might converge to a local minimum. Therefore, you must validate the estimated model. If the estimated model passes the validation test, you can use this model even if the SI Estimate ARMAX Model VI might locate only a local minimum.
The following equation shows the form of the ARMAX model.
A(z)y(k) = B(z)u(k - n) + C(z)e(k)| where | y(k) is the system outputs |
| u(k) is the system inputs | |
| n is the system delay | |
| e(k) is the system disturbance |
A(z), B(z), and C(z) are polynomial with respect to the backward shift operator z –1 and defined by the following equations.
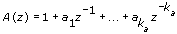
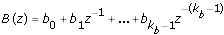
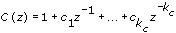
The following figure depicts the signal flow of an ARMAX model.
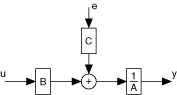
| where | u is the system inputs |
| e is the system disturbance | |
| y is the system outputs |
SISO
The following is the time domain equation for the ARMAX SISO model.
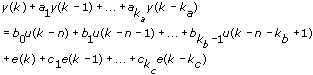
| where | ka is the A order |
| kb is the B order | |
| kc is the C order | |
| n is the system delay | |
| e(k) is the system disturbance |
Refer to the Estimate Polynomial Models VI in the labview\examples\System Identification\Getting Started\Parametric Estimation.llb for an example that demonstrates how to estimate ARMAX models for an unknown system.
