ARX Model Definitions (System Identification Toolkit)
When C(z), D(z), and F(z) equal 1, the general-linear polynomial model reduces to an autoregressive with exogenous terms (ARX) model. This model is the simplest model that incorporates the stimulus signal. However, the ARX model captures some of the stochastic dynamics as part of the system dynamics. In this model, the transfer function of the deterministic part G(z –1, θ) of the system and the transfer function of the stochastic part H(z –1, θ) of the system have the same set of poles. This coupling can be unrealistic. The system dynamics and stochastic dynamics of a system do not share the same set of poles all the time. You can reduce this disadvantage if the signal-to-noise ratio is high.
When the disturbance e(k) of a system is not white noise, the coupling between the deterministic and stochastic dynamics can bias the estimation of the ARX model. You can set the model order higher than the actual model order to minimize the estimation error, especially when the signal-to-noise ratio is low. However, increasing the model order can change some dynamic characteristics of the model, such as the stability of the model.
Use the SI Estimate ARX Model VI to estimate ARX models. The identification method for the ARX model is the least squares method, which is a special case of the prediction error method. The least squares method is the most efficient polynomial estimation method because this method solves linear regression equations in analytic form. Moreover, the solution is unique. Refer to the LabVIEW System Identification Toolkit Algorithm References manual for more information about the least squares and prediction error methods.
The following equation shows the form of the ARX model.
A(z)y(k) = B(z)u(k - n) + e(k)| where | u(k) is the system inputs |
| y(k) is the system outputs | |
| n is the system delay | |
| e(k) is the system disturbance |
A(z) and B(z) are polynomial with respect to the backward shift operator z –1 and defined by the following equations.
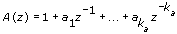
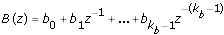
 |
Note The backward shift operator makes z –n u(k) = u(k - n). |
The following figure depicts the signal flow of an ARX model.
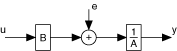
| where | u is the system inputs |
| e is the system disturbance | |
| y is the system outputs |
SISO
The following is the time domain equation for the ARX SISO model.
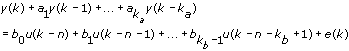
| where | kA order |
| kb is the B order | |
| n is the system delay | |
| e(k) is the system disturbance |
Refer to the Estimate Polynomial Models VI in the labview\examples\System Identification\Getting Started\Parametric Estimation.llb for an example that demonstrates how to estimate ARX models for an unknown system.
