Normalized Least Mean Squares (System Identification Toolkit)

The following equation defines a popular self-adjustable step-size μ(k) that you use in the normalized least mean squares (NLMS) algorithm.

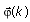represents the data vector. ε is a very small positive number that prevents the denominator from equaling zero when 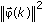approaches zero.

The step-size μ(k) is time-varying because the step-size changes with the time index k.

Substituting μ(k) into the parametric vector equation yields the following equation.

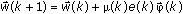
Compared to the least mean squares (LMS) algorithm, the NLMS algorithm is always stable if the step-size μ(k) is between zero and two, regardless of the statistical property of the stimulus signal u(k).

The procedure of the NLMS algorithm is the same as the LMS algorithm except for the estimation of the time-varying step-size μ(k).