Joint Input-Output Identification (System Identification Toolkit)

If you do not have any knowledge about the controller structure but the stimulus, response, and reference signals are all available, you can use the joint input-output identification approach to estimate the transfer function model of a plant in a closed-loop system. This approach uses the transfer functions from different input-output signal pairs to estimate a closed-loop system. The LabVIEW System Identification Toolkit implements the following two-stage method for the joint input-output approach.

1. Let T ₀(z) satisfy the following equation:
   
   

   

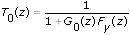
By manipulating two equations describing the feedback-path closed-loop system, you can rewrite u(k) as follows:

u(k) = T ₀(z)r(k) – F _y(z)T ₀(z)e(k)

Any open-loop model estimation method then can estimate T ₀(z) because r(k) and e(k) are uncorrelated signals. After you obtain the value of T ₀(z), you can compute û(k) = T ₀(z)r(k). You then can represent u(k) as follows:

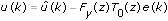
Using the previous equation, you obtain an input signal û(k), which is constructed from r(k) and is uncorrelated with the measurement noise.

2. By manipulating the equation y(k) = G ₀(z)u(k) + e(k), you can rewrite y(k) as follows:
   
   

   

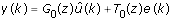
Because û(k) is uncorrelated with e(k), the original closed-loop model estimation problem between u(k) and y(k) becomes an open-loop problem between û(k) and y(k).

You use the same methodology to compute y(k) for a feedforward-path closed-loop system, where

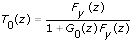
You rewrite y(k) as follows:

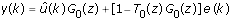
The two-stage method does not require you to know anything about the feedback or the controller structure and controller parameters. Also, you treat the closed-loop model estimation as an open-loop model estimation within each of the two steps. Therefore, you can use any method that works with open-loop models. Whether the real-world output noise is white noise or color noise, the two-stage method provides reliable estimations.