Box-Jenkins Model Definitions (System Identification Toolkit)
When A(z) equals 1, the general-linear polynomial model reduces to the Box-Jenkins model. This model provides a complete model of a system because this model represents disturbance properties separately from system dynamics. This model is useful when you have disturbances that enter late in the process, such as measurement noise on the output.
Use the SI Estimate BJ Model VI to estimate Box-Jenkins models. The identification method of the Box-Jenkins model is the prediction error method, which is the same as that of the ARMAX model.
The following equation shows the form of the Box-Jenkins model.
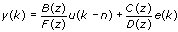
| where | y(k) is the system outputs |
| u(k) is the system inputs | |
| n is the system delay | |
| e(k) is the system disturbance |
B(z), C(z), D(z), and F(z) are polynomial with respect to the backward shift operator z -1 and defined by the following equations.
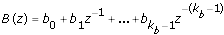
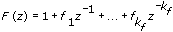
The following figure depicts the signal flow of a Box-Jenkins model.
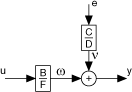
| where | u is the system inputs |
| e is the system disturbance | |
| y is the system outputs |
SISO
The following are the time domain equations for the Box-Jenkins SISO model.
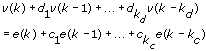
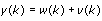
| where | kf is the F order |
| kb is the B order | |
| kc is the C order | |
| kd is the D order | |
| u(k) is the system input | |
| n is the system delay | |
| e(k) is the system disturbance |
Refer to the Estimate Polynomial Models VI in the labview\examples\System Identification\Getting Started\Parametric Estimation.llb for an example that demonstrates how to estimate Box-Jenkins models for an unknown system.
Open example
Browse related examples