Output-Error Model Definitions (System Identification Toolkit)
When A(z), C(z), and D(z) equal 1, the general-linear polynomial model reduces to the output-error model. This model describes the system dynamics separately from the stochastic dynamics. The output-error model does not use any parameters for simulating the disturbance characteristics.
Use the SI Estimate OE Model VI to estimate output-error models. The identification method of the output-error model is the prediction error method, which is the same as that of the ARMAX model. If the disturbance e(k) is white noise, all minima are global. However, a local minimum can exist if the disturbance is not white noise.
The following equation shows the form of the output-error model.
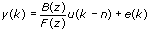
| where | y(k) is the system outputs |
| u(k) is the system inputs | |
| n is the system delay | |
| e(k) is the system disturbance |
B(z) and F(z) are polynomials with respect to the backward shift operator z –1 and defined by the following equations.
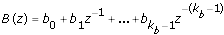
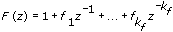
The following figure depicts the signal flow of an output-error model.
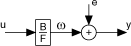
| where | u is the system inputs |
| e is the system disturbance | |
| y is the system outputs |
SISO
The following are the time domain equations for the output-error SISO model.
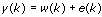
| where | kf is the F order |
| kb is the B order | |
| n is the system delay | |
| e(k) is the system disturbance |
Refer to the Estimate Polynomial Models VI in the labview\examples\System Identification\Getting Started\Parametric Estimation.llb for an example that demonstrates how to estimate Output-Error models for an unknown system.
Open example
Browse related examples