Spectral Analysis Method (System Identification Toolkit)

You can use the spectral analysis method with any input signal. However, the frequency bandwidth of the input signal must cover the range of interest.

Because the frequency response is the Fourier transform of the impulse response, applying the Fourier transform to both sides of the cross-correlation function yields the following equation.

Φ_uy(e^jω) = Φ_uu(e^jω)G(e^jω)

G(e^jω) is the frequency response of the system. Φ_uu(e^jω) is the auto-spectral density of the stimulus signal. Φ_uy(e^jω) is the cross-spectral density between the stimulus signal u(k) and the response signal y(k).

You then can use the following equation to compute the frequency response G(e^jω).

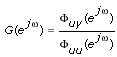
You can compute Φ_uu(e^jω) and Φ_uy(e^jω) by applying a fast Fourier transform (FFT) to the autocorrelation function R_uu and the cross-correlation function R_uy, respectively. The number of data points you need to compute the autocorrelation function R_uu and the cross-correlation function R_uy decreases as the lag τ increases. Therefore, R_uu and R_uy become inaccurate for a large lag τ. In this situation, you can apply a lag window to counter the effects of a large lag τ and improve the accuracy of the frequency response estimation.