Transfer Function Model Definitions (System Identification Toolkit)
You can use a transfer function to define either a continuous system or a discrete system. The following equations describe a continuous system and a discrete system, respectively, from which the transfer function is derived.
y(t) = G(s)u(t) + e(t)
y(k) = G(z)u(k) + e(k)
| where | y(t) and y(k) are the system outputs |
| G(s) and G(z) is the transfer function between the stimulus and the response | |
| u(t) and u(k) are the system inputs | |
| e(t) and e(k) are the system disturbance |
 |
Note Continuous models use the s variable to define time whereas discrete models use the z variable. |
SISO
The following is the equation for the continuous transfer function SISO model.
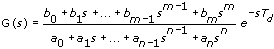
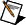 |
Note For transfer function SISO models based on frequency-domain data, Td equals zero. |
The following is the equation for the discrete-time transfer function SISO model.
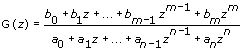
MISO
The following is the equation for the continuous transfer function MISO model.
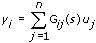
The following is the equation for the discrete-time transfer function MISO model.
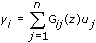
You can use the SI Estimate Transfer Function Model VI to estimate both continuous and discrete models. For discrete models, this VI implements the prediction error method. For continuous models, this VI internally performs the following three consecutive steps to estimate the model:
- Calculates a discrete model with the prediction error method.
- Applies the Zero-Order-Hold method to convert the discrete model to a continuous model.
- Uses the Gauss-Newton method to optimize the continuous model this VI converted in step 2.
You can use the SI Estimate Transfer Function Model from FRF VI to estimate both continuous and discrete SISO models in the frequency domain.
Transfer function models describe only the deterministic part of the system. For stochastic control, general-linear polynomial models commonly are used because these models separately describe the deterministic and stochastic parts of a system. However, in classical control engineering, the deterministic part of the system is more important than the stochastic part. Therefore, you can take advantage of the relationship between input and output signals of the transfer function model to describe the deterministic part of the system.