Determining Parameters for the Prediction Error Method (System Identification Toolkit)

The identification method for most of the polynomial models is the prediction error method. Determining the delay and model order for the prediction error method is typically a trial-and-error process. The following steps can help you obtain a suitable model. These steps are not the only methods you can use, nor are these steps a comprehensive procedure.

1. Obtain useful information about the model order by observing the number of resonance peaks in the nonparametric frequency response function. Normally, the number of peaks in the magnitude response equals half the order of A(z)F(z).
2. Obtain a reasonable estimate of the delay by observing the impulse response or by testing reasonable values in a medium-sized ARX model. Choose the delay that provides the best model fit based on prediction errors or another criterion.
3. Test various ARX model orders with this delay, choosing those orders that provide the best fit.
4. Reduce the model order by plotting the poles and zeros with confidence intervals and looking for potential cancellations of pole-zero pairs. The resulting model might be unnecessarily high in order because the ARX model describes both the system dynamics and noise properties using the same set of poles. The ARMAX, output-error, and Box-Jenkins models use the resulting orders of the poles and zeros as the B and F model parameters and the first- or second-order models for the noise characteristics.
5. Determine if additional signals influence the output if you cannot obtain a suitable model at this point. You can incorporate measurements of these signals as extra input signals.

If you still cannot obtain a suitable model, additional physical insight into the problem might be necessary. Compensating for nonlinear sensors or actuators and handling important physical nonlinearities often are necessary in addition to using a ready-made model.

From the prediction error standpoint, the higher the order of the model is, the better the model fits the data because the model has more degrees of freedom. However, you need more computation time and memory for higher orders. The parsimony principle says to choose the model with the smallest degree of freedom, or number of parameters, if all the models fit the data well and pass the verification test. The criteria to assess the model order therefore not only must rely on the prediction error but also must incorporate a penalty when the order increases. Akaike's Information Criterion (AIC), Final Prediction Error Criterion (FPE), and the Minimum Description Length Criterion (MDL) are criteria you can use to estimate the model order. The SI Estimate Orders of System Model VI implements the AIC, FPE, and MDL methods to search for the optimal model order in the range of interest. You also can plot the prediction error as a function of the model dimension and then visually find the minimum in the curve or apply an F-test to obtain an appropriate estimation of the model order.

Akaike's Information Criterion

The Akaike's Information Criterion (AIC) is a weighted estimation error based on the unexplained variation of a given time series with a penalty term when exceeding the optimal number of parameters to represent the system. For the AIC, an optimal model is the one that minimizes the following equation:

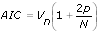
N is the number of data points, V_n is an index related to the prediction error, or the residual sum of squares, and p defines the number of parameters in the model.

Final Prediction Error Criterion

The Final Prediction Error Criterion (FPE) estimates the model-fitting error when you use the model to predict new outputs. For the FPE, an optimal model is the one that minimizes the following equation:

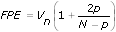
You want to choose a model that minimizes the FPE, which represents a balance between the number of parameters and the explained variation.

Minimum Description Length Criterion

The Minimal Description Length Criterion (MDL) is based on V_n plus a penalty for the number of terms used. For the MDL, an optimal model is the one that minimizes the following equation:

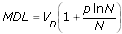
You want to choose a model that minimizes the MDL, which allows the shortest description of data you measure.