AR Model Definitions (System Identification Toolkit)

The autoregressive (AR) model does not include the dynamics between the system input and output. Therefore, the AR model is more suitable for representing signals rather than a system because a system generally has an input and an output. Time series analysis methods, such as power spectrum envelope estimation, prewhitening, and linear prediction coding, commonly use the AR model. Refer to the Time Series Analysis Tools User Manual at ni.com/manuals for more information about time series analysis methods.

Use the SI Estimate AR Model VI to estimate AR system models. The following equation shows the form of the AR model.

A(z)y(k) = e(k)

where	y(k) is the system outputs
	e(k) is the system disturbance

A(z) is polynomial with respect to the backward shift operator z ^–1 and defined by the following equation.

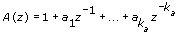
The following figure depicts the signal flow of an AR system model.

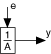
where	e is the system disturbance
	y is the system outputs

If you consider A(z) to be a filter, A(z)y(k) is the filtering of A(z) on the signal y(k). The result of the filtering is white noise e(k), as shown in the AR model equation. Hence, the filter A(z) also is known as the prewhitening filter. From the frequency-domain standpoint, the prewhitening filter A(z) suppresses the spectrum at frequencies where the magnitude of the spectrum is large. Suppressing the high-magnitude frequencies results in a flat spectrum.

As shown in the AR model equation, if you know the AR coefficients A(z) and the noise e(k), you can reconstruct the signal y(k). A(z) and e(k) completely characterize a signal. A(z) normally has a small number of coefficients. e(k) has a small dynamic range and requires a smaller number of bits for encoding. Therefore, you can use the AR model for compression purposes in a process known as linear prediction coding (LPC). Speech and vibration signal processing methods, such as compression and pattern recognition, commonly use LPC. You also can use A(z) and e(k) to estimate the power spectrum of the signal y(k).