Least Mean Squares (System Identification Toolkit)
The least mean squares (LMS) method uses the following equations to define the cost function J(k) = E[e 2(k)].
The parametric vector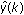 
updates according to the following equation.
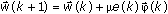
k is the number of iterations, μ is step-size, which is a positive constant, and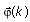 
is the data vector from the past input data u(k) and output data y(k). 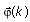is defined by the following equation.
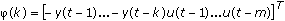
The following procedure describes how to implement the LMS algorithm.
- Initialize the step-size μ.
- Initialize the parametric vector
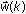using a small positive number ε.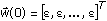
- Initialize the data vector
.
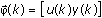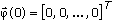
- For k = 1, update the data vector 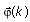based on
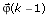and the current input data u(k) and output data y(k). - Compute the predicted response 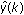using the following equation.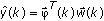
- Compute the error e( k) by solving the following equation.
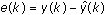
- Update the parameter vector .
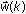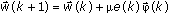
- Stop if the error is small enough, else set k = k + 1 and repeat steps 4–8.
The LMS algorithm is one of the most widely used and understood adaptive algorithms. Selecting the step-size μ is important with the LMS algorithm, because the selection of the step-size μ directly affects the rate of convergence and the stability of the algorithm. The convergence rate of the LMS algorithm is usually proportional to the step-size μ. The larger the step-size μ, the faster the convergence rate. However, a large step-size μ can cause the LMS algorithm to become unstable. The following equation describes the range of the step-size μ.
0 < μ < μ max
μ max is the maximum step-size that maintains stability in the LMS algorithm. μ max is related to the statistical property of the stimulus signal. A uniformly optimized step-size μ that achieves a fast convergence speed while maintaining the stability in the system does not exist, regardless of the statistical property of the stimulus signal. For better performance, use a self-adjustable step-size μ and the normalized least mean squares (NLMS) algorithm.