Kalman Filter (System Identification Toolkit)

The Kalman filter is a linear optimum filter that minimizes the mean of the squared error recursively. The convergence rate of the Kalman filter is relatively fast, but the implementation is more complex than that of LMS-based algorithms.

Recall that the equation J(k) = E[e ²(k)] defines the cost function. The following procedure lists the steps of the Kalman filter algorithm.

1. Initialize the parametric vector 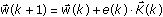using a small positive number ε.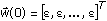
   
   

   

2. Initialize the data vector .
   
   

   

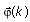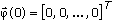
3. Initialize the k × k matrix P(0).
   
   

   

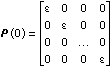
4. For k = 1, update the data vector 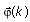based on 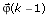and the current input data u(k) and output data y(k).
5. Compute the predicted response 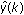by solving the following equation.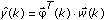
   
   

   

6. Compute the error e(k) by solving the following equation.
   
   

   

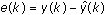
7. Update the Kalman gain vector 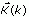defined by the following equation.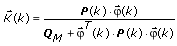
   
   

   

   
   
   Q _M is the measurement noise and P(k) is a k × k matrix whose initial value is defined by P(0) in step 3.
8. Update the parametric vector .
   
   

   

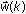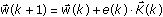
9. Update the P(k) matrix.
   
   

   

   
   
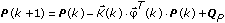
   Q_P is the correlation matrix of the process noise.
10. Stop if the error is small enough, else set k = k + 1 and repeat steps 4–10.