Indirect Identification (System Identification Toolkit)

The indirect identification approach, which estimates the transfer function model of a plant in a closed-loop system, first identifies the transfer function model of the closed-loop system based on the reference signal and the response signal. This approach then retrieves the transfer function model of the plant from the identified closed-loop system. The indirect identification approach can identify the transfer function of the plant accurately even when the signal-to-noise ratio (SNR) of the system is low and no matter whether the output noise is white noise or color noise. However, this approach requires prior knowledge about the controller of the system and the reference signal also must be available. In addition, any inaccuracy or nonlinearity of the controller in the system might affect estimating the model of the plant.

With indirect identification, you can use the following two equations to describe the feedback-path closed-loop system.

y(k) = G ₀(z)u(k) + e(k)

u(k) = r(k) – F _y(z)y(k)

where	G0(z) is the open-loop transfer function of the plant
	Fy(z)is the transfer function of a linear, time-invariant (LTI) controller
	u(k) is the stimulus signal of the system
	y(k) is the response signal of the system
	r(k) is the reference signal of the system
	e(k) is the output noise of the system

By combining the previous two equations, you can represent the closed-loop relationship with the following equation:

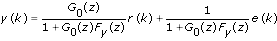
If you define G _cl as the closed-loop transfer function between the reference signal and the response signal, and let G _cl satisfy the following equation:

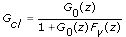
you can estimate G _cl with r(k) as the input and y(k) as the output using an open loop method, because r(k) and e(k) are uncorrelated. You then can calculate G ₀ after you calculate G _cl, as the following equation shows:

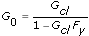
For feedforward-path closed-loop systems, you use the following two equations to describe the systems.

y(k) = G ₀(z)u(k) + e(k)

u(k) = [r(k) – y(k)]F _y(z)

By combining the previous two equations, you can represent the feedforward-path closed-loop relationship with the following equation:

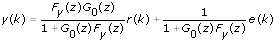
If you define G _cl as the feedforward-path closed-loop transfer function and let G _cl satisfy the following equation:

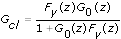
you can estimate G _cl with r(k) as the input and y(k) as the output using an open loop method, because r(k) and e(k) are uncorrelated. You then can calculate G ₀ after you calculate G _cl, as the following equation shows:

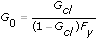
With indirect identification, you calculate G _cl by performing polynomial operations on G _o and F _y. Because of the limitations of polynomial operations, the orders of the numerator and denominator might change after manipulation. Thus, the SI Estimate Transfer Function Model VI or the SI Transfer Function Estimation ExpressVI, which you can use with the indirect identification approach, might return an error regarding the mismatch between the order you set and the order of the estimated model. In this case, you must adjust the tolerance setting of these two VIs so that the numerator and denominator orders match the orders you set. A larger tolerance facilitates zero-pole cancellations, which reduce the numerator and denominator polynomial orders.