LOI.BINOMIALE.NEG

Renvoie la distribution binomiale négative. LOI.BINOMIALE.NEG renvoie la probabilité qu'il y ait nombre_échecs échecs avant le succès N° nombre_succès, lorsque la probabilité constante d'un succès est probabilité_succès. Cette fonction est similaire à la distribution binomiale, excepté que le nombre de succès est fixé et que le nombre d'essais est variable. Comme dans la distribution binomiale, il est supposé que les essais sont indépendants.

Par exemple, vous devez trouver 10 personnes ayant des excellents réflexes, et vous savez que la probabilité qu'un candidat ait ces qualifications est de 0,3. LOI.BINOMIALE.NEG calcule la probabilité que vous ayez à interviewer un certain nombre de candidats non qualifiés avant de trouver 10 candidats qualifiés.

Syntaxe

LOI.BINOMIALE.NEG(nombre_échecs;nombre_succès;probabilité_succès)

nombre_échecs   représente le nombre d'échecs.

nombre_succès   représente le nombre de succès à obtenir.

probabilité_succès   représente la probabilité d'obtenir un succès.

Remarques

• nombre_échecs et nombre_succès doivent être >= 0.
• nombre_échecs et nombre_succès sont tronqués à leur partie entière.
• Si un des arguments n'est pas numérique, LOI.BINOMIALE.NEG renvoie la valeur d'erreur #VALEUR!.
• Si probabilité_succès < 0 ou si probabilité_succès > 1, LOI.BINOMIALE.NEG renvoie la valeur d'erreur #NOMBRE!.
• L'équation pour la distribution binomiale négative est :

  

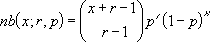
  où :

  x est nombre_échecs, r est nombre_succès et p est probabilité_succès.

Exemple

nombre_échecs	nombre_succès	probabilité_succès	Formule	Description (résultat)
10	5	0,25	=LOI.BINOMIALE.NEG([nombre_échecs];[nombre_succès];[probabilité_succès])	Distribution binomiale négative pour les arguments spécifiés (0,055049)