LOI.HYPERGEOMETRIQUE

Renvoie la probabilité d'une variable aléatoire discrète suivant une loi hypergéométrique. LOI.HYPERGEOMETRIQUE renvoie la probabilité d'un nombre donné de succès d'un échantillon, étant donnés la taille de l'échantillon, les succès de la population et la taille de la population. Utilisez LOI.HYPERGEOMETRIQUE pour des problèmes de population finie, où chaque observation est soit un succès soit un échec, et où chaque sous-ensemble d'une taille donnée est choisi avec une probabilité égale.

Syntaxe

LOI.HYPERGEOMETRIQUE(succès_échantillon;nombre_échantillon;succès_population;nombre_population)

succès_échantillon   représente le nombre de succès de l'échantillon.

nombre_échantillon   représente la taille de l'échantillon.

succès_population   représente le nombre de succès de la population.

nombre_population   représente la taille de la population.

Remarques

• Tous les arguments sont tronqués à des entiers.
• Si un des arguments n'est pas numérique, LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #VALEUR!.
• Si succès_échantillon < 0 ou si succès_échantillon est supérieur au plus petit des deux arguments nombre_échantillon et succès_population, LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #NOMBRE!.
• Si succès_échantillon est inférieur à la valeur la plus grande de 0 ou de (nombre_échantillon - nombre_population + succès_population), LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #NOMBRE!.
• Si nombre_échantillon < 0 ou si nombre_échantillon > nombre_population, LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #NOMBRE!.
• Si succès_population < 0 ou si succès_population > nombre_population, LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #NOMBRE!.
• Si nombre_population < 0, LOI.HYPERGEOMETRIQUE renvoie la valeur d'erreur #NOMBRE!.
• L'équation pour la distribution hypergéométrique est :

  

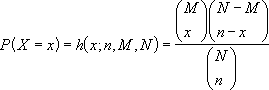
  où :

  x = succès_échantillon

  n = nombre_échantillon

  M = succès_population

  N = nombre_population

  LOI.HYPERGEOMETRIQUE est utilisée dans l'échantillonnage sans substitution à partir d'une population finie.

Exemple

Un échantillon de chocolats contient 20 pièces. Huit pièces sont au caramel et les douze autres sont aux noisettes. Si une personne choisit 4 pièces au hasard, la fonction suivante renvoie la probabilité que exactement une pièce soit au caramel.

succès_échantillon	nombre_échantillon	succès_population	nombre_population	Formule	Description (résultat)
1	4	8	20	=LOI.HYPERGEOMETRIQUE([succès_échantillon];[nombre_échantillon];[succès_population];[nombre_population])	Distribution hypergéométrique pour l'échantillon et la population (0,363261)