LOI.BINOMIALE

Renvoie la probabilité d'une variable aléatoire discrète suivant la loi binomiale. Utilisez LOI.BINOMIALE dans des problèmes avec un nombre fixe de tests ou d'essais, lorsque les résultats des tirages sont seulement des succès ou des échecs, lorsque les essais sont indépendants et que la probabilité de succès est constante tout au long de l'expérimentation. Par exemple, LOI.BINOMIALE peut calculer la probabilité que deux des trois bébés suivants soient des garçons.

Syntaxe

LOI.BINOMIALE(nombre_s;essais;probabilité_s;cumulée)

nombre_s   représente le nombre d'essais réussis.

essais   représente le nombre d'essais indépendants.

probabilité_s   représente la probabilité de succès de chaque essai.

Cumulative   représente une valeur logique déterminant le mode de calcul de la fonction : cumulatif ou non. Si cumulative est VRAI, alors LOI.BINOMIALE renvoie la fonction de distribution cumulative, qui est la probabilité qu'il y ait au plus nombre_s succès ; si cumulative est FAUX, elle renvoie la fonction de probabilité de masse, qui est la probabilité qu'il y ait exactement nombre_s succès.

Remarques

• nombre_s et essais sont tronqués à leur partie entière.
• Si nombre_s, essais ou probabilité_s ne sont pas des valeurs numériques, LOI.BINOMIALE renvoie la valeur d'erreur #VALEUR!.
• Si nombre_s < 0 ou nombre_s > essais, LOI.BINOMIALE renvoie la valeur d'erreur #NOMBRE!.
• Si probabilité_s < 0 ou probabilité_s > 1, LOI.BINOMIALE renvoie la valeur d'erreur #NOMBRE!.
• La fonction de probabilité de masse binomiale est :

  

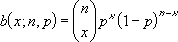
  où :

  

  est COMBIN(n,x).

   Remarque   La fonction COMBIN est utilisée ici pour illustrer la formule mathématique utilisée par la fonction LOI.BINOMIALE. Ce n'est pas une fonction que vous pouvez utiliser dans une liste.

  La distribution binomiale cumulative est :

  

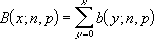
Exemple

nombre_s	essais	probabilité_s	Formule	Description (résultat)
6	10	0,5	=LOI.BINOMIALE([nombre_s];[essais];[probabilité_s];FAUX)	Probabilité que exactement 6 essais sur 10 soient des succès (0,205078)