INTERVALLE.CONFIANCE
Renvoie l'intervalle de confiance pour une moyenne de population avec une distribution normale. L'intervalle de confiance est une plage de chaque côté d'une moyenne échantillonnée. Par exemple, si vous commandez un produit par courrier, vous pouvez déterminer, avec un niveau spécifique de confiance, la date au plus tôt et la date au plus tard à laquelle le produit va arriver.
Syntaxe
INTERVALLE.CONFIANCE(alpha;écart-type;taille)
alpha représente le niveau critique utilisé pour calculer le niveau de confiance. Celui-ci est égal à 100*(1 - alpha) % ; en d'autres termes, un alpha de 0,05 indique un niveau de confiance de 95 %.
écart-type représente l'écart-type de la population pour la plage de données ; il est supposé connu.
taille représente la taille de l'échantillon.
Remarques
- Si un des arguments n'est pas numérique, INTERVALLE.CONFIANCE renvoie la valeur d'erreur #VALEUR!.
- Si alpha = 0 ou alpha = 1, INTERVALLE.CONFIANCE renvoie la valeur d'erreur #NOMBRE!.
- Si écart-type = 0, INTERVALLE.CONFIANCE renvoie la valeur d'erreur #NOMBRE!.
- Si taille n'est pas un entier, il est tronqué.
- Si taille < 1, INTERVALLE.CONFIANCE renvoie la valeur d'erreur #NOMBRE!.
- En supposant une valeur alpha égale à 0,05, il faut calculer la zone sous la courbe normale standard qui est égale à (1 - alpha), c'est-à-dire à 95 pour cent. Cette valeur est ± 1,96. Le niveau de confiance est donc :
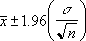
Exemple
Supposons que, sur un échantillon de 50 voyageurs, la durée moyenne du trajet vers le lieu de travail est de 30 minutes avec un écart-type de population de 2,5. On peut alors être sûr à 95 % que la moyenne de la population se trouve dans l'intervalle :
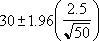
| alpha | écart-type | taille | Formule | Description (résultat) |
|---|---|---|---|---|
| 0,05 | 0,5 | 50 | =INTERVALLE.CONFIANCE([alpha];[écart-type];[taille]) | Intervalle de confiance pour une moyenne de population. En d'autres termes, la durée moyenne du trajet vers le lieu de travail est égale à 30 ± 0,692951 minutes, ou 29,3 à 30,7 minutes. (0,692951) |