LOI.GAMMA

Renvoie la probabilité d'une variable aléatoire suivant une loi Gamma. Vous pouvez utiliser cette fonction pour étudier des variables dont la distribution est susceptible d'être asymétrique. La loi gamma est couramment utilisée dans l'étude de files d'attente.

Syntaxe

LOI.GAMMA(x; alpha;bêta;cumulative)

x   représente la valeur à laquelle vous voulez évaluer la distribution

alpha   représente un paramètre de la distribution.

bêta   représente un paramètre de la distribution. Si bêta vaut 1, cette fonction renvoie la probabilité d'une variable aléatoire suivant une loi Gamma centrée réduite.

Cumulative   représente une valeur logique déterminant le mode de calcul de la fonction : cumulatif ou non. Si l'argument cumulative est VRAI, la fonction LOI.GAMMA renvoie la fonction de distribution cumulée ; si l'argument cumulative est FAUX, la fonction renvoie la fonction de probabilité de masse.

Remarques

• Si x, alpha ou bêta n'est pas numérique, LOI.GAMMA renvoie la valeur d'erreur #VALEUR!.
• Si x < 0, LOI.GAMMA renvoie la valeur d'erreur #NOMBRE!.
• Si alpha = 0 ou si bêta = 0, LOI.GAMMA renvoie la valeur d'erreur #NOMBRE!.
• L'équation pour la distribution gamma est :

  

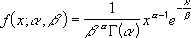
  La distribution gamma standard est :

  

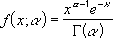
• Lorsque alpha = 1, LOI.GAMMA renvoie la distribution exponentielle avec :

  

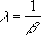
• Pour un entier positif n, lorsque alpha = n/2, bêta = 2 et cumulative = VRAI, LOI.GAMMA renvoie (1 - LOI.KHIDEUX(x)) avec n degrés de liberté.
• Lorsque alpha est un entier positif, LOI.GAMMA est également appelé distribution d'Erlang.

Exemple

x	alpha	bêta	Formule	Description (résultat)
10	9	2	=LOI.GAMMA([x];[alpha];[bêta];FAUX)	Distribution gamma des probabilités pour les arguments spécifiés (0,032639)
10	9	2	=LOI.GAMMA([x];[alpha];[bêta];VRAI)	Distribution gamma cumulée pour les arguments spécifiés (0,068094)