PrWin and Versus - Winning Probabilities
| prwin | versus | weighted prwin | enhanced prwin | |
| preflop/postflop | both | both | both | both |
| accuracy | depends on f$prwin_number_of_iterations | 100% exact | depends on f$prwin_number_of_iterations | depends on f$prwin_number_of_iterations |
| speed | depends on f$prwin_number_of_iterations | superfast (precomputed table) | depends on f$prwin_number_of_iterations | depends on f$prwin_number_of_iterations |
| handranges |
random only
(100% range) |
arbitrary handlists,
but usually fixed |
userdefined range, but simplified model |
arbitrary handrange,
userdefined |
| opponnents | 1-22, using f$prwin_number_of_opponents | 1 | 1-13, using f$prwin_number_of_opponents (weighted prwin will be disabled, if value > 13.) | nopponentsplaying |
| formula / DLL | all | all | all | DLL only |
Standard PrWin
Standard PrWin was the first way to calculate winning probabilities with WinHoldem. Just like so many other features of WinHoldem it is based on an oversimplified model, assuming a 100% range for all opponents, i.e. just random cards, no matter what.
This method has an obvious drawback: the calculated winning-percentages are way too optimistic.
Instead of improving that basic model a rude workaround got introduce: f$prwin_number_of_opponents, a function to adapt the number of opponents considered by the PrWin-Iterator. So instead of modelling hand-ranges for your opponents depending on the texture of the boards and the bettinglevel you had to do some guesswork about how many opponents to add to get the same numbers.
For an explanation about the required number of iterations see the chapter ”Iterations and Standard Deviation”. But as a rule of thumb 10.000 to 100.000 should give you reasonable numbers.
Versus
Versus is a capability introduced into WinHoldem in 2005 (and implemented in OH from startup) which allows the user to assess his probability of winning against a single opponent with a specified handlist. It does use large pre-computed tables and the result is substantially obtained by table lookup rather than the Monte Carlo iteration used for Prwin. It is much faster than Prwin, and the user can weight the result by selecting a suitable handlist for the opponent. It is thus a powerful tool for calculating good win probability against a single opponent.
Especially useful is the multiplexer-function
that looks up a numbered list depending on a range-function. For example the calculation of allin-equity could become as simple as
vs$multiplex$X$prwin // or prlos, prtie
##f$allin_equity_against_bigblind## vs$multiplex$f$bigblind_calling_range$prwin + 0.5 * vs$multiplex$f$bigblind_calling_range$prtie
Against multiple opponents its utility is much reduced, since the existence of the same cards in different opponent handlists is not allowed for the versus calculation, and combining the results from several independent versus assessments creates an increasingly inaccurate estimate as the number of opponents increases.
Weighted PrWin
Weighted Prwin does work similar to Standard PrWin, but enables you to model opponents handranges. It got developed by Matrix as part of his DLL and then contributed to OpenHoldem.
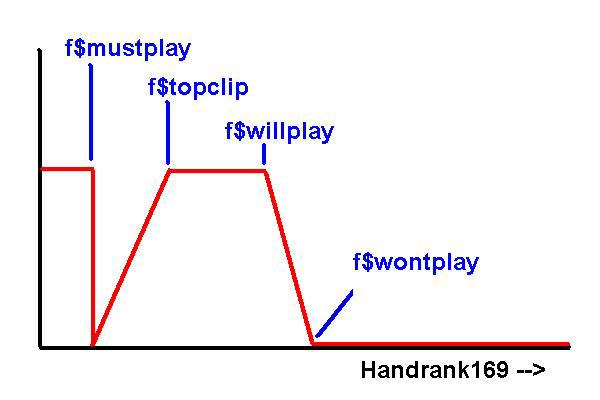
The hand-range of your opponent gets described by four parameters, each specifying a handrank169-value:
- f$mustplay: absolute premium-hands, that will never be folded by your opponent, even if the betting-action does not indicate a monster-hand. If you are dead-sure, that your opponent doesn’t slowplay aces, you can set f$mustplay to zero.
- f$topclip: the top of your opponents range, which will be played with certainty. Cards between f$topclip and f$mustplay will also be included, but with reduced probability.
- f$willplay: the bottom of your opponents range, which will be played with certainty.
- f$wontplay: the border to pure trash. Hands rated lower will never be played by your opponent. Hands between f$willplay and f$wontplay will be included in his range, but with reduced probability.
Ideally you would base the calculations of these points on the statistics for opponent betting pre-flop at various bet levels. This information is not currently available from OH (unless you use the PokerTracker capabilities), but the single most useful statistic, SingleMalt’s floppct, can be used. Using this to set f$willplay and f$wontplay gives the major advantage which a weighted prwin gives; the elimination of rags from the iterator calculations. A starting point might be something like:
##f$willplay## handsplayed<10 ? 72 : 180*floppct ##f$wontplay## f$willplay * 1.4
Weighted PrWin will fall back to Standard PrWin, when the parameters provided are unusable, e.g.
- if f$willplay is absent, or returns zero.
- if f$prwin_number_of_opponents is greater than 13.
The calculation will furthermore not weight the cards for an opponent who is BB and has limped into the flop. f$willplay will be increased internally if it is so low that the iterator cannot assign cards for all opponents from the available matching hands.
Weighted PrWin gives far better results than Standard PrWin, but the ability to specify handranges is still somewhat limited due to the ordering of hands according to their handrank-value. It is e.g. a bit hard to model playing tendencies or the preference for hands with low equity but good playability, like low pairs and suited connectors.
Furthermore the same range will be assumed for all opponents in the hand.
As the hand-ranges are more concrete than for Standard PrWin f$prwin_number_of_opponents should obviously return the correct number of opponents in the hand.
Enhanced PrWin
To overcome that limitations Enhanced PrWin got developed (again by Matrix). Enhanced PrWin does allow you to specify a probability for every single hand and thus gives you exact winning probabilities (provided you model the hand-ranges correctly). However — this mightiness causes some complexity and some labour. Advanced opponent modelling and calculating probabilities for every single hand is too complex for OH-script. Therefore this features is only available at the DLL-level and gets described in more detail in the chapter about DLL-programming.
Document generated by eLyXer 1.2.5 (2013-03-10) on 2015-06-27T00:12:55.125000