 Diagram Designer
Diagram Designer
 |
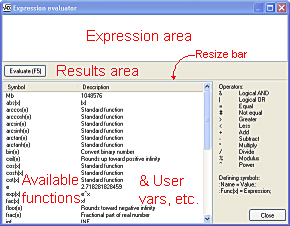
Expression Evaluator |
|
 |
The Diagram Designer Expression Evaluator is a powerful programmable calculator and equation plotter. Notable features are:
-
 trigonometric
functions
trigonometric
functions - hyperbolic functions
- logical operators
- named user variables can be created and used
- recursive descent parsing (ie. handles nested terms)
- equations can be programmed and used later
- multi-line programming with a single result
- some constants built-in, more can be added by user using expressions
- equation solving (roots, minimums, etc.) and plotting - plots can be inserted into diagrams
USAGE
The Expression Evaluator is used by entering statements in the expression area, then using Evaluate (F5) to evaluate the statements. Statements fall into the general format of:
- :Variable_name=variable_contents;
- :Function_name(function_variable)=expression_in_variable;
- expression_to_evaluate
Variable assignments and user functions (enclosed by : and ;) may used multiple times (in any order), but the expression to evaluate is a single expression and is the last line of the program. Note that variable names, function names (internal and external) and internal constants are case-sensitive; UserFunc is not the same as userfunc. Spaces in expressions and assignments should not be used, if possible. Note that the Expression Evaluator does not support the use of
- strings; it is numeric only
- comments. You may comment your code, but when using it (ie. pasting it into Expression Evaluator), comments must not be used.
After the program (ie. statements and expressions) is entered, pressing F5 (or clicking the button) will evaluate all statements (in order) and place the result in the results area in decimal, hexadecimal and binary format. Results can be highlighted and copied to the clipboard, if desired. Also expressions may be pasted into the expression area to save typing.
EXAMPLE
| Problem |
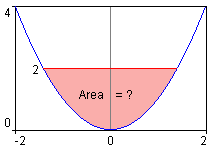
The formula Y=X2 determines a parabola, centered around the Y axis (ie. X=0). Imagine that 2 dimensional liquid is poured into the parabolic cup; find the cross-sectional area of that liquid, with the cup filled to a level of 2.
|
| Solution |
 Area
under the curve is calculated by integrating the function, with respect to X
(ie. ∫ƒ(x) dx, where ƒ(x) = x2), yielding 1/3*X3.
If liquid were to be poured into the parabolic cup formed by
the equation, the cross sectional area of that liquid (2 dimensional)
can be calculated using the area under the parabola, for the limits of X,
and the area of a simple rectangle. First, the value of N must
be calculated - the point on the X axis where the level of 2 units occurs.
Since Y=N2 and Y = 2, then N = sqrt(2). This can be
proven by using an "adjusted" equation Y=X2 - 2 which shifts
the parabola down 2 units. This means that the value of X which yields
a Y of 0 (the fill point) is equal to N. The proof of this can be
input into Expression Evaluator as: Area
under the curve is calculated by integrating the function, with respect to X
(ie. ∫ƒ(x) dx, where ƒ(x) = x2), yielding 1/3*X3.
If liquid were to be poured into the parabolic cup formed by
the equation, the cross sectional area of that liquid (2 dimensional)
can be calculated using the area under the parabola, for the limits of X,
and the area of a simple rectangle. First, the value of N must
be calculated - the point on the X axis where the level of 2 units occurs.
Since Y=N2 and Y = 2, then N = sqrt(2). This can be
proven by using an "adjusted" equation Y=X2 - 2 which shifts
the parabola down 2 units. This means that the value of X which yields
a Y of 0 (the fill point) is equal to N. The proof of this can be
input into Expression Evaluator as:
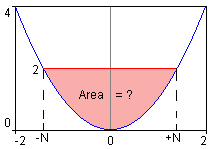
This means: if the equation root = √2 then return true (ie. 1) as the result, else return 0 (false). Pasting this into the expression area and evaluating confirms this result. The simple rectangle area (includes the desired area, plus the area under the curve) = (√2 - (-√2 ) ) * 2. Reducing this further; this can be written as:
The area under the curve (from -N to N), then can be calculated (with a little reducing) as:
Subtract this from the rectangle, then yields the final program as: :N=sqrt(2); Evaluating this program yields a final result of 3.771236166328, the area of the liquid. |
REFERENCE
OPERATORS Operators are listed in order of precedence. Note: symbol spelling is case sensitive
| Equation solving, etc. | RESULT/Comments |
| & | logical AND. For testing purposes, any non-zero number is considered true. |
| | | logical OR |
| = | equality (test). Tests return 0 (false) or 1 (true) |
| # | inequality (test) |
| > | greater than (test) |
| < | less than (test) |
| + | addition |
| - | subtraction, or negation (as in -5) |
| * | multiplication |
| / | division |
| % | modulus. Result is the remainder of integer division, eg. 16.1%3.03 is equivalent to 16/3. Remainder (result) in this example is 1. |
| ^ | power (ie. Y^X = YX). Raises any real (ie. Y) to the power of any other real (X). |
CONSTANTS Note: symbol spelling is case sensitive
| CONSTANT | RETURNS/Comments |
| e | 2.718281828459 |
| inf | infinity (≈ 1 / 0) |
| kb | kilobyte = 1024 |
| Mb | megabyte = 1048576 |
| pi | = 3.14159265359 |
FUNCTIONS Note: symbol spelling is case sensitive
| FUNCTION - trigonometric | RETURNS/Comments |
| cos(x) | cosine of X (in radians) |
| arccos(x) | inverse cosine of X, returns radians |
| sin(x) | sine of X (in radians) |
| arcsin(x) | inverse sine of X, returns radians |
| tan(x) | tangent of X (in radians) = sin(x) / cos(x) |
| arctan(x) | inverse tangent of X, returns radians |
| cot(x) | cotangent of X (in radians) = cos(x) / sin(x) |
| FUNCTION - hyperbolic | RETURNS/Comments |
| cosh(x) | hyperbolic cosine = (ex + e-x) / 2 |
| arccosh(x) | inverse hyperbolic cosine of X |
| sinh(x) | hyperbolic sine = (ex - e-x) / 2 |
| arcsinh(x) | inverse hyperbolic sine of X |
| tanh | hyperbolic tangent of X = sinh(x) / cosh(x) |
| arctanh(x) | inverse hyperbolic tangent of X |
| FUNCTION - rounding | RETURNS/Comments |
| ceil(x) | nearest integer, rounding up towards positive infinity |
| floor(x) | nearest integer, rounding down towards negative infinity |
| frac(x) | fractional part of real number |
| round(x) | nearest integer, up or down |
| FUNCTION - random no. | RETURNS/Comments |
| rand(x) | real number in range 0..X This is a white noise random number generator. No apparent pattern of the random numbers should be detected. |
| randn(x) | return Gaussian random numbers, with X as a standard deviation. Gaussian random numbers are clustered around 0 in the typical Gaussian standard distribution curve. This function returns random numbers clustered around 0, with a standard deviation of X. |
| FUNCTION - logarithmic | RETURNS/Comments |
| exp(x) | natural exponential function = ex |
| ln(x) | natural logarithm (base e) |
| log10(x) | common logarithm (base 10) |
| log2(x) | logarithm (base 2) where x = 2log2(x) |
| FUNCTION - misc | RETURNS/Comments |
| abs(x) | absolute value of X (value or variable) |
| bin(x) | converts X (binary integer) to decimal |
| fac(x) | factorial function, eg. fac(4) = 4 * 3 * 2 * 1 = 24 |
| sqrt(x) | square root of X |
EQUATION SOLVING, ETC. Note: symbol spelling is case sensitive
| FUNCTION | RETURNS/Comments |
| num.Guess | Expression Evaluator uses numeric methods to solve for minimums, etc. This variable houses the initial guess used in numeric computations (initial default on program startup = 0.500000001). |
| num.argmin(expression,x) | Find X that minimizes the expression given. Example: num.argmin((x-1)*(x-1)+4,x) will yield 0.999999999976 as a result. The equation is a parabola, centered on the X=1 axis and shifted 4 units up. The result is effectively 1.0(internal rounding errors will cause the last few decimal places to change), the value of X at the minima of the curve. |
| num.min(expression,x) | Find the minimum value for the expression show.
This is similar to num.argmin, but returns the function of X (or other
variable) at the minima. Example: num.min((x-1)*(x-1)+4,x) will yield 4 as a result, the value of ƒ(x) at the minima. |
| num.root(expression,x) | Find the root (value of X where ƒ(x)=0) of the
expression. Example: num.root(x^2-5*x+4,x) yields 1.0 as a result. This is verified by showing that 12 - 5 * 1 + 4 = 0. In fact, there is another root at 4.0; this can be found by setting num.Guess to 6 prior to computation. This can be accomplished by the following program: :num.Guess=6; which yields 4 as the result. |
| num.solve(equation,x) | Solves for the value of the target variable.
This is similar to num.root, but solves for X (or other variable) yielding
values other than 0. Example: num.solve(y^2-5*y+4=14,y) yields 6.531128874149 as a result. This can be proved by pasting the following into Expression Evaluator and evaluating: :y=6.531128874149; The result (13.999999999998) is effectively 14, with rounding errors, proving the equation's solution. |
PLOTTING Note: symbol spelling is case sensitive
| Equation solving, etc. | RETURNS/Comments |
| plot(expression,x) | Plots any expression, if possible. Try
pasting this into the expression area:
The above plots the equation Y=1/X, including both the positive and negative portions. Once evaluated, the plot window opens displaying the plot, and allowing different X limits (range). The plot can be copied to the clipboard, then pasted into Diagram Designer as a metafile. Left-clicking on any point of the curve (as near a possible) and hovering there will display the coordinates (approximate) of that point. In the examples above for num.argmin, etc., try pasting the samples into Expression Evaluator, but change the function to plot - you can see the answer! |
 |

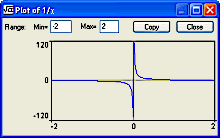 plot(1/x,x)
plot(1/x,x)