Owning Palette: State-Space Model Analysis VIs
Installed With: Control Design and Simulation Module
Calculates the Observability Matrix of the State-Space Model. You can use the observability matrix N to determine if the given system is observable. A system of order n is observable if N is full rank, meaning the rank of N is equal to n. This VI also determines if the given system is detectable. A system is detectable if all the unstable eigenvalues are observable.
 Place on the block diagram | Find on the Functions palette |
 | State-Space Model contains a mathematical representation of and information about the system for which this VI determines the observability matrix. | ||||||
 | Tolerance is the threshold this VI uses to determine if the observability matrix is column rank deficient. The default is 1E–6. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Observability Matrix is the matrix O computed for a system with a system matrix A and output matrix C.
The matrix O is defined by the following equation: | ||||||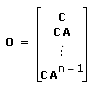
 | If Is Observable? is TRUE, the system is observable. | ||||||
| If Is Detectable? is TRUE, the system is detectable. A system is detectable if all unstable eigenvalues are observable. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Observability Matrix Details
This VI does not support delays unless the delays are part of the mathematical model that represents the dynamic system. To account for the delays in the synthesis of the controller, you must incorporate the delays into the mathematical model of the dynamic system using the CD Convert Delay with Pade Approximation VI (continuous models) or the CD Convert Delay to Poles at Origin VI (discrete models). Refer to the LabVIEW Control Design User Manual for more information about delays and the limitations of Pade Approximation.