CD Calculate Integrals with Matrix Exponential VI

	Ac specifies an n x n state matrix, where n is the number of states.
	Bc specifies an n x m input matrix, where m is the number of inputs. The default value is the transpose of A.
	Qc specifies the state weight matrix. Q must be symmetric and positive semi-definite.
	Rc specifies the input weight matrix. R must be symmetric and positive definite. The default is an identity matrix of appropriate dimensions.
	Nc specifies the state-input cross weight matrix. The value of Nc must be such that the matrix (Qc–Nc*inv(Rc)*Nc) is positive semi-definite. The default value of Nc is an empty matrix of appropriate dimensions.
	Ts specifies the upper limit of the integral of the matrix this VI calculates. Refer to the Details section for the matrix this VI calculates.
	error in describes error conditions that occur before this VI or function runs. The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code. Use exception control to treat what is normally an error as no error or to treat a warning as an error. Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node. status is TRUE (X) if an error occurred before this VI or function ran or FALSE (checkmark) to indicate a warning or that no error occurred before this VI or function ran. The default is FALSE. code is the error or warning code. The default is 0. If status is TRUE, code is a nonzero error code. If status is FALSE, code is 0 or a warning code. source specifies the origin of the error or warning and is, in most cases, the name of the VI or function that produced the error or warning. The default is an empty string.
	Qd returns the 1 x 1 block of the matrix this VI calculates. Refer to the Details section for the matrix this VI calculates.
	Rd returns the 2 x 2 block of the matrix this VI calculates. Refer to the Details section for the matrix this VI calculates.
	Nd returns the 1 x 2 block of the matrix this VI calculates. Refer to the Details section for the matrix this VI calculates.
	error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces. Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error. status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred. code is the error or warning code. If status is TRUE, code is a nonzero error code. If status is FALSE, code is 0 or a warning code. source describes the origin of the error or warning and is, in most cases, the name of the VI or function that produced the error or warning.

CD Calculate Integrals with Matrix Exponential Details

This VI calculates the outputs according to the following equations:

where

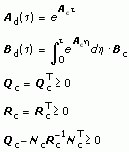
If you interpret the inputs to this VI as describing information about a continuous system model, you can interpret the outputs of this VI as discretized versions of these inputs, where Ts is the sampling time.

For example, if you make the following assumptions:

• Ac represents the continuous system matrix that describes the states of the system.
• Bc represents the continuous input matrix that relates the inputs to the states.
• Qc represents the continuous cost matrix penalizing the system states. This matrix also can represent the continuous process noise spectral intensity matrix.
• Rc represents the continuous cost matrix penalizing the system inputs. This matrix also can represent the continuous measurement noise spectral intensity matrix.
• Nc represents the continuous cost matrix penalizing the cross product between the system states and the system inputs. This matrix also can represent the continuous cross-spectral intensity matrix between the process noise and the measurement noise.
• Ts represents the sampling time this VI uses to discretize the continuous matrices Ac, Bc, Qc, Rc, and Nc.

• Qd is the discrete equivalent of Qc.
• Rd is the discrete equivalent of Rc.
• Nd is the discrete equivalent of Nc.