Owning Palette: Dynamic Characteristics VIs
Installed With: Control Design and Simulation Module
Returns the covariance of the outputs and/or states when Gaussian white noise excites the input model. The data type you wire to the State-Space Model input determines the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Place on the block diagram Place on the block diagram |  Find on the Functions palette Find on the Functions palette |
CD Covariance Response (State-Space)

 | State-Space Model contains a mathematical representation of and additional model information about the system of which this VI determines output covariance. | ||||||
 | Gaussian White Noise Covariance is a symmetric, positive semi-definite matrix N that specifies the covariance of the noise exciting the system. The dimensions of this parameter also must be consistent with the system model. Refer to the Details section for the definition of this parameter when the model is continuous or discrete. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Output Covariance is the covariance matrix of the output y of the system when Gaussian white noise with covariance N excites the system. | ||||||
 | State Covariance is the covariance matrix X of the state vector x when Gaussian white noise with covariance N excites the system that the State-Space Model represents. State Covariance is valid only when the model is in state-space form. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Covariance Response (Transfer Function)

 | Transfer Function Model contains a mathematical representation of and information about the system of which this VI determines output covariance. | ||||||
 | Gaussian White Noise Covariance is a symmetric, positive semi-definite matrix N that specifies the covariance of the noise exciting the system. The dimensions of this parameter also must be consistent with the system model. Refer to the Details section for the definition of this parameter when the model is continuous or discrete. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Output Covariance is the covariance matrix of the output y of the system when Gaussian white noise with covariance N excites the system. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Covariance Response (Zero-Pole-Gain)

 | Zero-Pole-Gain Model contains a mathematical representation of and information about the system of which this VI determines output covariance. | ||||||
 | Gaussian White Noise Covariance is a symmetric, positive semi-definite matrix N that specifies the covariance of the noise exciting the system. The dimensions of this parameter also must be consistent with the system model. Refer to the Details section for the definition of this parameter when the model is continuous or discrete. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Output Covariance is the covariance matrix of the output y of the system when Gaussian white noise with covariance N excites the system. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Covariance Response Details
The model must be stable for covariance to exist. You can use the CD Stability VI to determine model stability.
Continuous Models
This VI assumes continuous state-space models are of the following form:
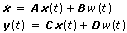
For continuous models, the Gaussian White Noise Covariance is defined as
Nd(t – t) = E{w(t) . wT(t)}
The Output Covariance is defined as
E{y(t) . yT(t)}
The State Covariance is defined as
E{x(t) . xT(t)}
This VI uses the following equations to calculate the outputs:
Output Covariance = CXCT, where X is the solution to the continuous Lyapunov equation AX+XAT = –BNBT.
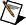 | Note If D does not equal zero, the Output Covariance is infinite. |
State Covariance = X, which is the solution to the continuous Lyapunov equation.
Discrete Models
This VI assumes discrete state-space models are of the following form:
x(k+1) = Ax(k) + Bw(k)
y(k) = Cx(k) + Dw(k)
For discrete models, the Gaussian White Noise Covariance is defined as
Ndkl = E[wk . wTl]
The Output Covariance is defined as
E{y(k) . yT(l)}
The State Covariance is defined as
E{x(k) . xT(l)}
This VI uses the following equation to calculate the outputs:
Output Covariance = CXCT+DNDT, where X is the solution to the discrete Lyapunov equation AXAT–X = –BNBT.
State Covariance = X, which is the solution to the discrete Lyapunov equation.
| where | y is the output vector |
| x is the state vector | |
| A is the state matrix | |
| B is the input matrix | |
| C is the output matrix | |
| D is the direct transmission matrix | |
| X is the solution to the continuous or discrete Riccati equation | |
| w is the Gaussian white noise | |
| t is continuous time | |
| k is discrete time | |
| d(t – t) is the Dirac delta function | |
| dkl is the Kronecker delta function | |
| E{} is the expected value or mean of the enclosed term(s) |
This VI does not support delays unless the delays are part of the mathematical model that represents the dynamic system. To account for the delays when calculating the dynamic characteristics of a system, you must incorporate the delays into the mathematical model of the dynamic system using the CD Convert Delay with Pade Approximation VI (continuous models) or the CD Convert Delay to Poles at Origin VI (discrete models). Refer to the LabVIEW Control Design User Manual for more information about delays and the limitations of Pade Approximation.





