CD Norm VI
Owning Palette: Dynamic Characteristics VIs
Installed With: Control Design and Simulation Module
Calculates the infinity-norm and 2-norm of linear time-invariant (LTI) systems. The 2-norm is infinite for unstable systems and for state-space systems whose D matrix is not equal to zero. The data type you wire to the State-Space Model input determines the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Place on the block diagram | Find on the Functions palette |
CD Norm (State-Space)
 | State-Space Model contains a mathematical representation of and information about the system of which this VI determines the norm. | ||||||
 | Type specifies the method for calculating the norm.
| ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Norm returns the value of ||H||2 or ||H|| , depending on the method specified in Type.
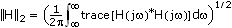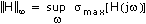  The 2-norm is the RMS of the output when white noise of unit intensity excites the system. The infinity-norm is the maximum magnification of the frequency response of the system. | ||||||
| Frequency returns the value, in rad/s, at which this VI evaluates ||H||. Frequency is undefined for ||H||2 and has a value of NaN.
| ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Norm (Transfer Function)
| Transfer Function Model contains a mathematical representation of and information about the system of which this VI determines the norm. | ||||||
| Type specifies the method for calculating the norm.
| ||||||
| error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
| Norm returns the value of ||H||2 or ||H||, depending on the method specified in Type.
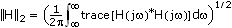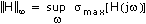The 2-norm is the RMS of the output when white noise of unit intensity excites the system. The infinity-norm is the maximum magnification of the frequency response of the system. | ||||||
| Frequency returns the value, in rad/s, at which this VI evaluates ||H||. Frequency is undefined for ||H||2 and has a value of NaN.
| ||||||
| error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Norm (Zero-Pole-Gain)
| Zero-Pole-Gain Model contains a mathematical representation of and information about the system of which this VI determines the norm. | ||||||
| Type specifies the method for calculating the norm.
| ||||||
| error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
| Norm returns the value of ||H||2 or ||H||, depending on the method specified in Type.
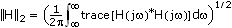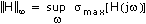The 2-norm is the RMS of the output when white noise of unit intensity excites the system. The infinity-norm is the maximum magnification of the frequency response of the system. | ||||||
| Frequency returns the value, in rad/s, at which this VI evaluates ||H||. Frequency is undefined for ||H||2 and has a value of NaN.
| ||||||
| error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Norm Details
This VI does not support delays unless the delays are part of the mathematical model that represents the dynamic system. To account for the delays when calculating the dynamic characteristics of a system, you must incorporate the delays into the mathematical model of the dynamic system using the CD Convert Delay with Pade Approximation VI (continuous models) or the CD Convert Delay to Poles at Origin VI (discrete models). Refer to the LabVIEW Control Design User Manual for more information about delays and the limitations of Pade Approximation.