Owning Palette: State Feedback Design VIs
Installed With: Control Design and Simulation Module
Calculates the optimal steady-state feedback gain matrix K that minimizes a linear quadratic cost function you specify. You can use this VI to calculate K for a continuous or discrete state-space model. You also can use this VI to calculate automatically a discrete K for a continuous state-space model. This calculation uses a specified sampling time and an associated continuous cost function. You must manually select the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Place on the block diagram Place on the block diagram |  Find on the Functions palette Find on the Functions palette |
CD Linear Quadratic Regulator (LQR)

 | Weighting Type determines the type of cost function this VI minimizes.
Refer to the Details section for the cost function equations.
| ||||||
 | State-Space Model contains a mathematical representation of and information about the system for which this VI calculates state feedback optimal gain. | ||||||
 | Q specifies a symmetric, positive semi-definite matrix that penalizes the state vector x in the cost function. If you specify a cost function that weights the model outputs, Q penalizes the output vector y in the cost function. | ||||||
 | R specifies a symmetric, positive definite matrix that penalizes the input vector u in the cost function. | ||||||
 | N specifies a matrix of appropriate dimensions that penalizes the cross-product between the input and state vectors. If you do not wire a value to this parameter, this VI sets N to an appropriately-sized matrix of zeros. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Optimal Gain (K) is the resulting state feedback gain matrix K that minimizes the cost function. | ||||||
 | Eigenvalues are the poles of the resulting closed-loop system. The poles are equal to the eigenvalues of A–BK. | ||||||
 | Riccati Solution (X) returns the symmetric, positive semi-definite solution X to the continuous or discrete algebraic Riccati equation, depending whether the model you wire to the State-Space Model input of this VI is continuous or discrete. However, the Discretized LQR instance of this VI always returns the solution to the discrete algebraic Riccati equation. Refer to the Details section for the definitions of the Riccati equations. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Linear Quadratic Regulator (Discretized LQR)

 | Weighting Type determines the type of cost function this VI minimizes.
Refer to the Details section for the cost function equations.
| ||||||
 | Continuous State-Space Model specifies the continuous state-space model for which this VI designs a discrete-time LQR controller. | ||||||
 | Q specifies a symmetric, positive semi-definite matrix that penalizes the state vector x in the cost function. If you specify a cost function that weights the model outputs, Q penalizes the output vector y in the cost function. | ||||||
 | R specifies a symmetric, positive definite matrix that penalizes the input vector u in the cost function. | ||||||
 | N specifies a matrix of appropriate dimensions that penalizes the cross-product between the input and state vectors. If you do not wire a value to this parameter, this VI sets N to an appropriately-sized matrix of zeros. | ||||||
 | error in describes error conditions that occur before this VI or function runs.
The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code.
Use exception control to treat what is normally an error as no error or to treat a warning as an error.
Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.
| ||||||
 | Sampling Time specifies the discrete sampling time this VI uses to discretize the continuous state-space model and cost function. The resulting discrete Optimal Gain (K) is associated with this sampling time. The default value is 1 second. | ||||||
 | Optimal Gain (K) is the resulting state feedback gain matrix K that minimizes the cost function. | ||||||
 | Eigenvalues are the poles of the resulting closed-loop system. The poles are equal to the eigenvalues of A–BK. | ||||||
 | Riccati Solution (X) returns the symmetric, positive semi-definite solution X to the continuous or discrete algebraic Riccati equation, depending whether the model you wire to the State-Space Model input of this VI is continuous or discrete. However, the Discretized LQR instance of this VI always returns the solution to the discrete algebraic Riccati equation. Refer to the Details section for the definitions of the Riccati equations. | ||||||
 | error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces.
Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.
|
CD Linear Quadratic Regulator Details
The value you specify for the Weighting Type parameter determines the cost function this VI minimizes. The cost function also depends on whether the model is continuous or discrete.
Continuous Models
State Weighting
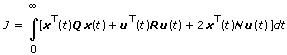
Output Weighting, Dim[Q] = Ny
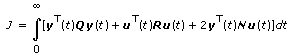
Output Weighting, Dim[Q] = Nx
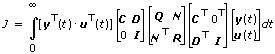
For continuous models, Optimal Gain (K) = R–1[BTX+NT].
This VI solves the continuous algebraic Riccati equation, defined as ATX+XA–[XB+N]R–1[XB+N]T+Q = 0.
Discrete Models
State Weighting
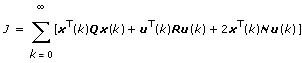
Output Weighting, Dim[Q] = Ny
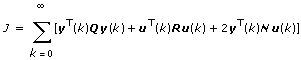
Output Weighting, Dim[Q] = Nx
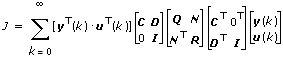
For discrete models, Optimal Gain (K) = [BTXB+R]–1[BTXA+NT].
This VI solves the discrete algebraic Riccati equation, defined as ATXA–[ATXB+N][BTXB+R]–1][ATXB+N]T+Q = X.
Matrix Restrictions
For continuous models, you must be able to stabilize the pair 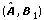 .
.
| where | 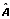 = A–BR–1NT = A–BR–1NT |
| B1 is the full-rank factorization of G = BR–1BT, that is, G = B1BT1 and rank[G] = rank[B1] |
For discrete models, you must be able to stabilize the pair 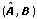 .
.
For continuous and discrete models, you must be able to detect the pair 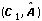 .
.
| where | C1 is the full-rank factorization of H = Q–NR–1NT, that is, H = C1CT1 and rank[H] = rank[C1] |
Q and R must satisfy the following relationships, respectively:
Q = QT ≥ 0
R = RT > 0
N must satisfy the following relationship:
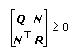
| where | u is the input |
| y is the output | |
| x is the states | |
| t is continuous time | |
| k is discrete time | |
| Q is the state-weighting matrix | |
| R is the input-weighting matrix | |
| N is the cross-weighting matrix between the states and inputs | |
| B is the input matrix | |
| C is the output matrix | |
| D is the direct transmission matrix | |
| I is the identity matrix | |
| X is the solution to the continuous or discrete algebraic Riccati equation |
Discretized Linear Quadratic Regulator
This instance converts the A, B, C, and D matrices using the numerical integration method as proposed by Van Loan. Refer to the following sources for more information about this method.
- G.F. Franklin, J.D. Powell, and M. Workman, Digital Control of Dynamic Systems, 3rd ed. Menlo Park, CA: Addison Wesley, 1997.
- C.F.V. Loan, "Computing integrals involving the matrix exponential," IEEE Transactions on Automatic Control, vol. 23, no. 3, pp. 395–404, June 1978.
This VI does not support delays unless the delays are part of the mathematical model that represents the dynamic system. To account for the delays in the synthesis of the controller, you must incorporate the delays into the mathematical model of the dynamic system using the CD Convert Delay with Pade Approximation VI (continuous models) or the CD Convert Delay to Poles at Origin VI (discrete models). Refer to the LabVIEW Control Design User Manual for more information about delays and the limitations of Pade Approximation.





