CD Convert Continuous Stochastic to Discrete VI

Control Design VI and Function

Owning Palette: Stochastic Systems VIs

Installed With: Control Design and Simulation Module

Converts a continuous stochastic state-space model and the associated continuous noise model to a discrete stochastic state-space model and discrete noise model.

Details

Place on the block diagram

Find on the Functions palette

Continuous Stochastic State-Space Model specifies a mathematical representation of a continuous stochastic system.

Continuous Second-Order Statistics Noise Model specifies a continuous mathematical representation of the noise model of the Continuous Stochastic State-Space Model. A noise model defines the expected behavior of the noise vectors w and v. You can use the CD Construct Noise Model VI to construct a noise model for a given stochastic state-space system.

Sampling Time (s) specifies the discrete sampling time of the Discrete Stochastic State-Space Model. The default value is 1 second.

Method specifies the method this VI uses to calculate the discrete equivalent of the process noise covariance matrix Q.

0	Truncation of Taylor Series— Computes the discrete equivalent of the process noise covariance matrix by using the Truncation of Taylor Series Expansion method.
1	Numerical Integration (default)—Computes the discrete equivalent of the process noise covariance matrix by using the numerical integration method as proposed by Van Loan.

error in describes error conditions that occur before this VI or function runs. The default is no error. If an error occurred before this VI or function runs, the VI or function passes the error in value to error out. This VI or function runs normally only if no error occurred before this VI or function runs. If an error occurs while this VI or function runs, it runs normally and sets its own error status in error out. Use the Simple Error Handler or General Error Handler VIs to display the description of the error code. Use exception control to treat what is normally an error as no error or to treat a warning as an error. Use error in and error out to check errors and to specify execution order by wiring error out from one node to error in of the next node.

	status is TRUE (X) if an error occurred before this VI or function ran or FALSE (checkmark) to indicate a warning or that no error occurred before this VI or function ran. The default is FALSE.
	code is the error or warning code. The default is 0. If status is TRUE, code is a nonzero error code. If status is FALSE, code is 0 or a warning code.
	source specifies the origin of the error or warning and is, in most cases, the name of the VI or function that produced the error or warning. The default is an empty string.

Discrete Stochastic State-Space Model returns a mathematical representation of the discrete equivalent of the Continuous Stochastic State-Space Model.

Discrete Second-Order Statistics Noise Model returns a mathematical representation of the discrete equivalent of the Continuous Second-Order Statistics Noise Model.

error out contains error information. If error in indicates that an error occurred before this VI or function ran, error out contains the same error information. Otherwise, it describes the error status that this VI or function produces. Right-click the error out front panel indicator and select Explain Error from the shortcut menu for more information about the error.

	status is TRUE (X) if an error occurred or FALSE (checkmark) to indicate a warning or that no error occurred.
	code is the error or warning code. If status is TRUE, code is a nonzero error code. If status is FALSE, code is 0 or a warning code.
	source describes the origin of the error or warning and is, in most cases, the name of the VI or function that produced the error or warning.

CD Convert Continuous Stochastic to Discrete Details

This VI assumes the noise vectors w and v are temporally uncorrelated. This VI also assumes the Sampling Time T you specify is much smaller than the Shannon period of the input signal u(t). Therefore, the following relationship is true:

u(t) ≈ u(kT), kT ≤ t < (k + 1)T

where t is continuous time and k is discrete time.

This VI assumes the Continuous Stochastic State-Space Model is of the following form:

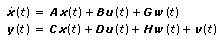
This VI also assumes the Continuous Second-Order Statistics Noise Model is of the following form:

E{w(t)} = m_w(t)

E{w(t) · w^T(τ)} = Q(t) · δ(t – τ)

E{v(t)} = m_v(t)

E{v(t) · v^T(τ)} = R(t) · δ(t – τ)

E{w(t) · v^T(τ)} = N(t) · δ(t – τ)

where d(t) is the Dirac delta function. This function is defined as d(t) = ∞ when x = 0; d(t) = 0 when x ≠ 0.

This VI returns the Discrete Stochastic State-Space Model in the following form:

x[(k + 1]T] = A_dx(kT) + B_du(kT) + n(kT)

y(kT) = C_dx(kT) + D_du(kT) + r(kT), k = 0, 1, 2 ...

where

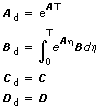
n(kT) and r(kT) are the discrete equivalents of the noise vectors.

This VI returns the Discrete Second-Order Statistics Noise Model in the following form:

E{n(kT)} = [A_d – I]A^–1Gm_w(kT)

E{n(kT) · n^T(lT)} = P(kT)δ(kT – lT), k, l = 0, 1, 2 ...

E{r(kT)} = Hm_w + m_v(kT)

E{r(kT) · r^T(lT)} = S(kT)δ(kT – lT)

E{n(kT) · r^T(lT)} = O(kT)δ(kT – lT)

where

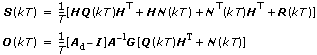
If you specify Numerical Integration for the Method parameter, then

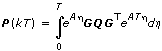
If you specify Truncation of TSE for the Method parameter, then

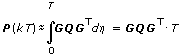
where	n is the number of states
	m is the number of inputs
	r is the number of outputs
	x is the state vector.
	u is the input vector.
	y is the output vector.
	w is the process noise vector.
	v is the observation noise vector.
	A is an n × n state matrix of the given system.
	B is an n × m input matrix of the given system.
	C is an r × n output matrix of the given system.
	D is an r × m direct transmission matrix of the given system.
	G is a matrix relating w to the states.
	H is a matrix relating w to the outputs.
	Q is the auto-covariance matrix of w.
	R is the auto-covariance matrix of v.
	N is the cross-covariance matrix between w and v.
	E{} denotes the expected mean or value of the enclosed term(s).

This approximation becomes less accurate as the value of T increases.

previous page start next page