IIR Direct Form Structures (Digital Filter Design Toolkit)

The transfer function of an infinite impulse response (IIR) filter is defined as follows:

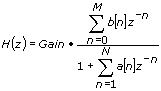
where z is a complex variable, M is the order of the numerator, N is the order of the denominator, a is the set of reverse coefficients, and b is the set of forward coefficients.

IIR Direct Form I

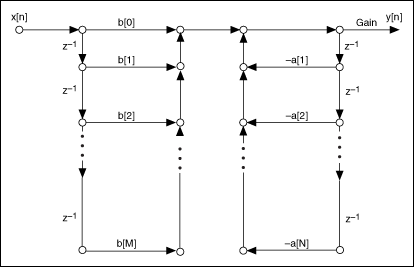
The IIR Direct Form I structure is the most straightforward IIR structure from a filter transfer function perspective. The following figure represents the IIR Direct Form I structure. Refer to the Understanding Filter Structure Graphs topic for information that helps you read and understand a filter structure graph.

Note  This figure and the following figures show a special case when N = M.

IIR Direct Form II

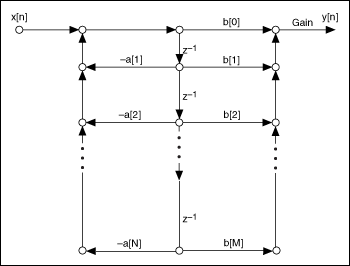
The following figure represents the IIR Direct Form II structure. You can see that this structure contains fewer mathematical operations and delays.

IIR Direct Form I Transposed

The following figure represents the IIR Direct Form I Transposed structure.

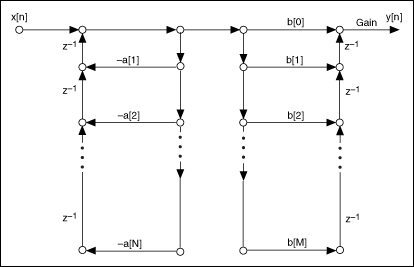
IIR Direct Form II Transposed

The following figure represents the IIR Direct Form II Transposed structure.

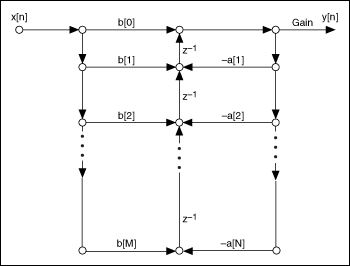
The IIR Direct Form I and Form II Transposed structures implement forward coefficients first. The Form I Transposed and Form II structures implement reverse coefficients first. Using Form I and Form II and their transposed structures has the same advantages and disadvantages as using the FIR Direct Form and FIR Direct Form Transposed structures. The IIR Direct Form structures usually require few mathematical operations. However, the sensitivity to finite word length effects limits the use of this form in fixed-point implementations. Use the IIR Cascaded Second-Order Sections Form structures to alleviate finite word length effects.