Group Delay and Phase Delay (Digital Filter Design Toolkit)
For a filter with a frequency response of H(ejω), the phase delay response 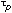 is defined by the following equation:
is defined by the following equation:
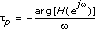
The group delay response 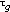 is defined as the negative derivative of the phase response ω, as shown in the following equation:
is defined as the negative derivative of the phase response ω, as shown in the following equation:

Both the group delay and phase delay are in samples.
For a generalized linear phase filter with arg[H(ejω)] = – ω+β, the group delay is represented by the following equation:
ω+β, the group delay is represented by the following equation:
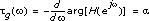
The phase delay is represented by the following equation:
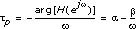
You can represent the phase delay as the time delay in samples experienced by each frequency component of the input signal. The filter is represented by the following illustration:

The filter H(ejω) shifts all frequency components by a phase β and then filters the signal with a new filter Hnew(ejω) that has a phase of – ω. You can interpret the group delay as the time delay in samples experienced by each frequency component through the new filter Hnew(ejω).
ω. You can interpret the group delay as the time delay in samples experienced by each frequency component through the new filter Hnew(ejω).
Linear phase filters are characterized by a constant group delay. The deviation of the group delay from a constant value within the passband indicates the degree of nonlinearity in the phase. Use the group delay to analyze the linearity of a filter.