Design Methods (Digital Filter Design Toolkit)

The LabVIEW Digital Filter Design Toolkit provides the following finite impulse response (FIR) filter design methods.

• Kaiser Window
• Dolph-Chebyshev Window
• Equi-Ripple FIR

The Kaiser Window method and the Dolph-Chebyshev Window method allows you to obtain the filter coefficients directly from the analytical equations, so these methods are easier to use than the Equi-Ripple FIR method, which also is known as the Remez design method, but the Equi-Ripple FIR method yields optimal filters and often produces the best results for most FIR filter design problems.

In addition to the FIR-based methods, the Digital Filter Design Toolkit supports the following infinite impulse response (IIR) filter design methods.

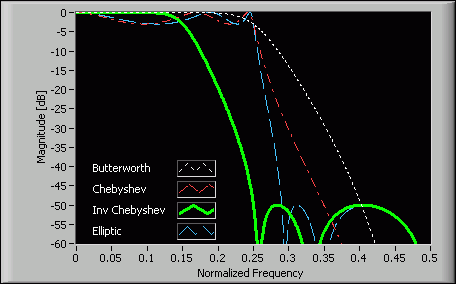
• Butterworth
• Chebyshev
• Inverse Chebyshev
• Elliptic

The following figure illustrates the magnitude responses of a typical lowpass filter designed by the four IIR filter design methods. Each filter has the same numerator and denominator order values.

The following table summarizes the main features of the four IIR-based design methods so you can determine the IIR filter design method to use.

IIR Filter	Ripple in Passband?	Ripple in Stopband?	Transition Bandwidth for a Fixed Order	Order for Given Filter Specifications
Butterworth	No	No	Widest	Highest
Chebyshev	Yes	No	Narrower	Lower
Inverse Chebyshev	No	Yes	Narrower	Lower
Elliptic	Yes	Yes	Narrowest	Lowest