Cells
The cell is the atomic element of a cube, or the unique logical intersection of one member from every dimension associated with the cube. Essentially, a cube is composed of cells organized by measures, levels, and dimensions.
For example, the cube described by the following diagram has a single shaded cell.
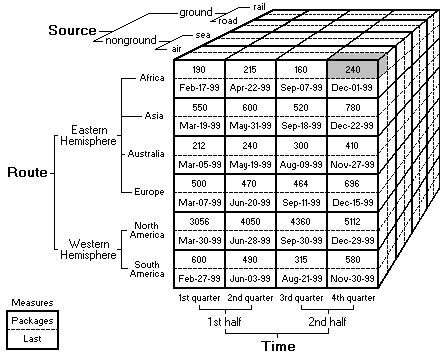
The shaded cell is the intersection of the following members and dimensions:
- The air member of the Source dimension.
- The Africa member of the Route dimension.
- The 4th quarter member of the Time dimension.
- The Packages member of the Measures dimension.
The value in the cell can be obtained from a number of sources. In the preceding example, the value in the cell is derived from the fact table of the cube, as all of the specified members are leaf members; a leaf member, hierarchically speaking, has no members below it.
However, a cell can be specified with
For example, the intersection of the following members and dimensions refers to a cell whose value is supplied by aggregation:
- The air member of the Source dimension.
- The Africa member of the Route dimension.
- The 2nd half member of the Time dimension.
- The Packages member of the Measures dimension.
The 2nd half member of the Time dimension is a nonleaf member, so all of the members associated to it must be selected and aggregated, as shown in the following diagram.
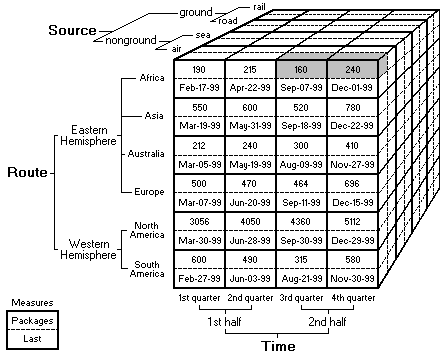
Assuming the aggregations for the 3rd quarter and 4th quarter members are summations, the value of the specified cell is the total of all of the cells shaded in the preceding diagram.
Some nonleaf members, called data members, can have intrinsic data associated with them, as well as data derived from the aggregation of members below the nonleaf member. For more information about data members, see Data Members.
The cell values derived for members employed by custom members, custom rollups, and member groups are handled in a similar fashion. Cell values derived for calculated members, however, are based entirely on the Multidimensional Expressions (MDX) expression used to define the calculated member; there may be no actual cell data involved.
Additionally, the value of a cell can be derived by a formula executed for a specific set of cells, through the use of calculated cells. Calculated cells provide a great deal of flexibility in performing speculative analysis by supplying the ability to selectively apply formulas to specific cells in a section of the cube, or subcube, based on a condition the cells in the subcube must first fulfill.
Empty Cells
Not every cell in a cube must contain a value; there can be intersections in a cube that have no data. These intersections, called empty cells, occur frequently in cubes, because not every intersection of dimensions can contain a corresponding record in a fact table. The ratio of empty cells in a cube to the total number of cells in a cube is often referred to as the sparsity of a cube.
For example, the cube shown in the following diagram is similar to examples in this topic.

However, in this example, there were no air shipments to Africa for the third quarter or to Australia for the fourth quarter. Therefore, there is no data in the fact table to support the intersections of those dimensions and measures, so the cells at those intersections are empty.
In Microsoft® SQL Server™ 2000 Analysis Services, an empty cell is a cell with special qualities. Because empty cells can skew the results of crossjoins, counts, and so on, many MDX functions supply the ability to ignore empty cells for the purposes of the result generation.
For more information about empty cells, see Working with Empty Cells.