NNV
Returnerer netto nåverdi for en investering med en diskonteringsrente og en rekke periodiske kontantstrømmer (negative verdier) og inntekter (positive verdier).
Syntaks
NNV(rente;verdi1;verdi2;...)
Rente er rentesatsen i hele perioden.
Verdi1; verdi2; ... er 1 til 29 argumenter som representerer innbetalinger og inntekter.
- Verdi1; verdi2; ... må ha lik avstand i tid, og finne sted i slutten av hver periode.
- NNV bruker rekkefølgen for argumentene verdi1; verdi2;... til å tolke rekkefølgen av kontantstrømmer. Pass på at du setter inn innbetalingene og inntektene i riktig rekkefølge
- Argumenter som er tall, tomme, logiske verdier eller tekstrepresentasjoner av tall, telles med. Argumenter som er feilverdier eller tekst som ikke lar seg konvertere til tall, ignoreres.
Obs!
- NNV-investeringen begynner én periode før datoen for kontantstrømmen i verdi1, og slutter med den siste kontantstrømmen i listen. Beregningene av NNV er basert på fremtidige kontantstrømmer. Hvis den første kontantstrømmen skjer i begynnelsen av perioden, må den første verdien legges til resultatet av NNV, og ikke inkluderes blant verdi-argumentene. Hvis du vil ha mer informasjon om dette, se eksemplene nedenfor.
- Hvis n er lik antall kontantstrømmer i listen med verdier, er formelen for NNV:
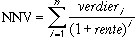
- NNV ligner på funksjonen NÅVERDI. Hovedforskjellen mellom NÅVERDI og NNV er at NÅVERDI tillater kontantstrømmer som begynner i slutten eller begynnelsen av perioden. Til forskjell fra de variable NNV-kontantstrømmene, må NÅVERDI-kontantstrømmene være konstante gjennom hele investeringsperioden. Hvis du vil ha mer informasjon om annuiteter og økonomiske funksjoner, kan du se funksjonen NÅVERDI
- NNV er også beslektet med funksjonen IR (intern rentabilitet). IR er renten når NNV er lik null: NNV(IR(...); ...) = 0.
Eksempel 1
I følgende eksempel:
- er Rente lik den årlige diskontorenten.
- Verdi1 er startkostnaden for investeringen om ett år fra i dag.
- Verdi2 er avkastning fra første år.
- Verdi3 er avkastning fra andre år.
- Verdi4 er avkastning fra tredje år.
| Rente | Verdi1 | Verdi2 | Verdi3 | Verdi4 | Formel | Beskrivelse (Resultat) |
|---|---|---|---|---|---|---|
| 10% | -10000 | 3000 | 4200 | 6800 | =NNV([Rente]; [Verdi1]; [Verdi2]; [Verdi3]; [Verdi4]) | Netto nåverdi for denne investeringen (1 188,44) |
I foregående eksempel inkluderes den første kostnaden på kr 10 000 som en av verdiene, fordi innbetalingen skjer på slutten av den første perioden.
Eksempel 2
I følgende eksempel:
- er Rente lik den årlige diskontorenten. Dette kan representere renten for inflasjonen eller rentesatsen for en konkurrerende investering.
- Verdi1 er startkostnaden for investeringen om ett år fra i dag.
- Verdi2 er avkastning fra første år.
- Verdi3 er avkastning fra andre år.
- Verdi4 er avkastning fra tredje år.
- Verdi5 er avkastning fra fjerde år.
- Verdi6 er avkastning fra femte år.
| Rente | Verdi1 | Verdi2 | Verdi3 | Verdi4 | Verdi5 | Verdi6 | Formel | Beskrivelse (Resultat) |
|---|---|---|---|---|---|---|---|---|
| 8% | 40000 | 8000 | 9200 | 10000 | 12000 | 14500 | =NNV(Rente; [Verdi2]; [Verdi3]; [Verdi4]; [Verdi5]; [Verdi6])+[Verdi1] | Netto nåverdi for denne investeringen (1 922,06) |
| 8% | 40000 | 8000 | 9200 | 10000 | 12000 | 14500 | =NNV(Rente; [Verdi2]; [Verdi3]; [Verdi4]; [Verdi5]; [Verdi6]; -9000)+[Verdi1] | Netto nåverdi for denne investeringen, med et tap i det sjette året på 9000 (-3 749,47) |
I foregående eksempel skal du ikke ta med den første kostnaden på kr 40 000 som en av verdiene, fordi innbetalingen skjer i begynnelsen av den første perioden.