Discrete Stochastic State-Space Function

Owning Palette: Discrete Linear Systems Functions

Installed With: Control Design and Simulation Module

Implements a discrete-time, linear, stochastic state-space system. You define the system model by specifying the input, output, state, and direct transmission matrices. You also specify the matrices relating the process noise to the system states and outputs.

If you use the Internal Noise instance of this function, this function generates samples of the noise vectors using the model you wire to the Second-Order Statistics Noise Model input. If you use the External Noise instance of this function, you can use the CD Correlated Gaussian Random Noise VI to generate samples of the noise vectors.

Details  

Dialog Box Options

Block Diagram Inputs

Block Diagram Outputs

Place on the block diagram

Find on the Functions palette

Dialog Box Options

Parameter	Description
Polymorphic instance	Specifies whether this function uses internally-generated random samples of Gaussian-distributed noise vectors or externally-generated noise or disturbances. The default is Internal Noise.
Feedthrough	Configures the function to be either a Direct or Indirect feedthrough function. Enable this control by selecting Stochastic State-Space Model from the Parameters list and then selecting Terminal from the Parameter source pull-down menu. If you select Configuration Dialog Box from the Parameter source pull-down menu, LabVIEW disables this control and calculates the feedthrough behavior automatically. Refer to the Details section for a description of the parameters that determine the feedthrough behavior of this function.
Parameters	Lists all the parameters associated with this function. Select a parameter from this list to configure the parameter. When you select a parameter, the parameter and its associated Parameter source control appear in the Parameter Information section of the configuration dialog box.
Preview	Displays a graphical preview, if available, of the function output or configuration.
Parameter Information	Contains the parameters you can configure for this function. You must select a parameter from the Parameters list to make that parameter and its associated Parameter source control visible in the Parameter Information section of the configuration dialog box.
Parameter source	Specifies whether you configure this parameter using the Configuration Dialog Box or a Terminal on the simulation diagram. The default value is Configuration Dialog Box. If you select Terminal, LabVIEW displays an input for that parameter on the simulation diagram, and you can wire values to that input to configure this function programmatically. If you select Configuration Dialog Box, LabVIEW removes that input from the simulation diagram. You then must set the value for this parameter inside the configuration dialog box.
reset?	Specifies whether to restart the calculation from any initial values you provide. The default is FALSE.
Stochastic State-Space Model	Specifies a mathematical representation of a stochastic system. You can construct a stochastic state-space model using the CD Construct Stochastic Model VI. A—Specifies the system matrix that describes the dynamics of the states of the system. B—Specifies the input matrix that relates the inputs to the states. G—Specifies the matrix that relates the process noise vector to the model states. C—Specifies the output matrix that relates the outputs to the states. D—Specifies the transmission matrix that relates the inputs to the outputs. H—Specifies the matrix that relates the process noise vector to the model outputs. Sampling Time (s)—Specifies the sampling time of the system model and determines whether the model represents a continuous-time or discrete-time system. If the model represents a continuous-time system, Sampling Time (s) must equal zero. If the model represents a discrete-time system, Sampling Time (s) must be greater than zero and equal to the sampling rate, in seconds, of the discrete system. The default is –1. If you specify a value of –1, this function inherits the discrete time step you specify for the simulation diagram. Otherwise, the value of Sampling Time (s) must be a multiple of the discrete time step you specify for the simulation diagram. This limitation applies only if you place this function inside a Simulation Loop. Note  If you use the inputs to create a continuous-time system, setting the Sampling Time (s) to a value greater than zero does not yield the discrete-time equivalent of the system. You must use the CD Convert Continuous Stochastic to Discrete VI to convert the continuous-time system to the discrete-time equivalent of the system.
Second-Order Statistics Noise Model	Specifies a mathematical representation of the noise model of a stochastic state-space model. You can create a noise model using the CD Construct Noise Model VI. This option is available only if you select Internal Noise from the Polymorphic instance pull-down menu. E{w}—Specifies the expected value or mean of the process noise vector. The default is 0. Q—Specifies the covariance matrix of the process noise vector. The default is 0.01. E{v}—Specifies the expected value or mean of the measurement noise vector. The default is 0. R—Specifies the covariance matrix of the measurement noise vector. The default is 0.1. N—Specifies the cross-covariance matrix between the process noise vector and the measurement noise vector. If these noise vectors are uncorrelated, N is a matrix of zeros. The default is 0.
sample skew (s)	Specifies the length of time by which you want to delay the execution of this function. The default value is 0. The value of this parameter must satisfy the following relationship: 0 ≤ sample skew (s) ≤ Sampling Time
Initial State x(0)	Specifies the initial state of the model. If you do not specify a value for this parameter, this function assumes an initial state of 0.

Block Diagram Inputs

Parameter	Description
reset?	Specifies whether to restart the calculation from any initial values you provide. The default is FALSE.
Stochastic State-Space Model	Specifies a mathematical representation of a stochastic system. You can construct a stochastic state-space model using the CD Construct Stochastic Model VI. A—Specifies the system matrix that describes the dynamics of the states of the system. B—Specifies the input matrix that relates the inputs to the states. G—Specifies the matrix that relates the process noise vector to the model states. C—Specifies the output matrix that relates the outputs to the states. D—Specifies the transmission matrix that relates the inputs to the outputs. H—Specifies the matrix that relates the process noise vector to the model outputs. Sampling Time (s)—Specifies the sampling time of the system model and determines whether the model represents a continuous-time or discrete-time system. If the model represents a continuous-time system, Sampling Time (s) must equal zero. If the model represents a discrete-time system, Sampling Time (s) must be greater than zero and equal to the sampling rate, in seconds, of the discrete system. The default is –1. If you specify a value of –1, this function inherits the discrete time step you specify for the simulation diagram. Otherwise, the value of Sampling Time (s) must be a multiple of the discrete time step you specify for the simulation diagram. This limitation applies only if you place this function inside a Simulation Loop. Note  If you use the inputs to create a continuous-time system, setting the Sampling Time (s) to a value greater than zero does not yield the discrete-time equivalent of the system. You must use the CD Convert Continuous Stochastic to Discrete VI to convert the continuous-time system to the discrete-time equivalent of the system.
Second-Order Statistics Noise Model	Specifies a mathematical representation of the noise model of a stochastic state-space model. You can create a noise model using the CD Construct Noise Model VI. This option is available only if you select Internal Noise from the Polymorphic instance pull-down menu. E{w}—Specifies the expected value or mean of the process noise vector. The default is 0. Q—Specifies the covariance matrix of the process noise vector. The default is 0.01. E{v}—Specifies the expected value or mean of the measurement noise vector. The default is 0. R—Specifies the covariance matrix of the measurement noise vector. The default is 0.1. N—Specifies the cross-covariance matrix between the process noise vector and the measurement noise vector. If these noise vectors are uncorrelated, N is a matrix of zeros. The default is 0.
sample skew (s)	Specifies the length of time by which you want to delay the execution of this function. The default value is 0. The value of this parameter must satisfy the following relationship: 0 ≤ sample skew (s) ≤ Sampling Time
Initial State x(0)	Specifies the initial state of the model. If you do not specify a value for this parameter, this function assumes an initial state of 0.
Input u(k)	Specifies the control action this function applies to the model. If you specify a vector of zeros for Input u(k), this function does not apply a control action.
Process Noise w(k)	Specifies the process noise vector. This input is available only if you select External Noise from the Polymorphic instance pull-down menu.
Measurement Noise v(k)	Specifies the measurement noise vector. This input is available only if you select External Noise from the Polymorphic instance pull-down menu.

Block Diagram Outputs

Parameter	Description
Output y(k)	Returns the values of the model output(s) at time k. The length of this vector is equal to the number of model outputs.
State x(k+1)	Returns the values of the model state(s) at time k + 1. The length of this vector is equal to the number of model states.
State x(k)	Returns the values of the model state(s) at time k. The length of this vector is equal to the number of model states.

Discrete Stochastic State-Space Details

Internal Noise

This function adapts to changes in the Stochastic State-Space Model and the Second-Order Statistics Noise Model, as long as the model dimensions do not change. Therefore, you can use this function to simulate linear time-variant (LTV) stochastic state-space models.

If you set the Parameter source to Terminal for the Second-Order Statistics Noise Model input, this function uses the Second-Order Statistics Noise Model to obtain the values of E{w(k)}, E{v(k)}, Q(k), R(k), and N(k). The following equations define these terms:

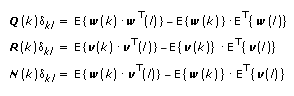
where	δkl is the Kronecker delta function. The following equations defines this function: δkl = 1 when k = l; δkl = 0 when k ≠ l.
	w(k) is the process noise vector.
	v(k) is the measurement noise vector.
	Q(k) is the covariance matrix of w(k).
	R(k) is the covariance matrix of v(k).
	N(k) is the cross-covariance matrix of w(k) and v(k). If these noise vectors are uncorrelated, N(k) is a matrix of zeros.
	E{} denotes the expected mean of the enclosed term(s).

This function also uses the Second-Order Statistics Noise Model to generate Gaussian-distributed temporally-uncorrelated random samples of w(k) and v(k) at each time step.

External Noise

This function adapts to changes in the Stochastic State-Space Model, as long as the model dimensions do not change. Therefore, you can use this function to simulate linear time-variant (LTV) stochastic state-space models.

Use the CD Correlated Gaussian Random Noise VI to generate external random samples of Gaussian-distributed noise vectors. You can use this VI and the Process Noise w(k) and Measurement Noise v(k) inputs of the Discrete Stochastic State-Space function to simulate the following conditions:

• Deterministic systems excited by deterministic disturbance vectors w(k) and v(k).
• Stochastic systems excited by stochastic noise vectors w(k) and v(k). These stochastic noise vectors can be zero-mean or nonzero-mean, stationary or nonstationary, and can have any density distribution.
• Deterministic or stochastic systems excited by w(k) and v(k), where one of these vectors is a deterministic disturbance and the other is a stochastic noise.

Feedthrough Behavior

The value you specify for the D matrix of the Stochastic State-Space Model parameter determines the feedthrough behavior of this function.

• If the D matrix is nonzero, all input/output pairs have direct feedthrough behavior.
• If the D matrix is zero, the following input/output pairs have indirect feedthrough behavior.
  • Input u(k) — Output y(k)
  • Input u(k) — State x(k)
  The remaining input/output pairs have direct feedthrough behavior.

When you use the configuration dialog box to configure the D matrix, LabVIEW verifies that the feedthrough behavior is correct. For example, if you set the Feedthrough parameter to Indirect, and you set the D matrix to nonzero, LabVIEW changes the Feedthrough parameter to Direct.

If you specify the value of the D matrix programmatically by wiring a value to the parameter terminal, LabVIEW does not adjust the feedthrough behavior for you. You must ensure that you specify the proper feedthrough behavior for the value of the D matrix that you specify.