Curve Fitting > Introduction
A mathematical model consists of a general equation representing the time course of the signal (or part of the signal) under study. For instance, the decay of many signals (e.g. synaptic currents) can be represented by an exponential function
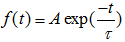 ,
,
where A is the amplitude of the signal and is the decay time constant. Expressed as above, the equation is quite general applying to any signal, depending on the values of the parameters A and .
In order to determine whether the equation actually does provide a good model of the signal decay it is necessary to find the parameter values which provides the best match (or fit) of the theoretical curve to an actual signal. This can be done using the process know as iterative curve fitting. Starting with initial guesses for the parameters, the theoretical curve is compared with the experimental data points, the parameters are adjusted to try to improve the fit, and the process is repeated until no more improvement can be obtained.
The quality or goodness of the fit between theoretical curve and the data is determined from the sum of the squared differences (S) between a set of n data points, y(i) (i=1..n), and the theoretical curve, f(i), computed at the same sample time points, i.e.
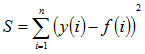
The best fit is found by repeatedly computing S, at each iteration adjusting the equation parameters using a strategy to minimise S. The best fit parameters are the ones which yield a minimum value of S. WinWCP uses a modified Levenberg-Marquardt least squares minimisation algorithm (the SSQMIN routine, developed by Kenneth Brown at the University of Cincinnatti). (A more detailed discussion of curve fitting algorithms can be found in Chapter 6 of Dempster, 1993.)