Returnerer den hyperbolske sinus til et tall.
Syntaks
SINH(tall)
Tall er ethvert reelt tall.
Kommentarer
Formelen for den hyperbolske sinus er:
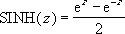
Eksempel 1
Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.
- Opprett et tomt regneark.
- Velg eksemplet i hjelpeemnet.

Velg et eksempel fra Hjelp
- Trykk CTRL+C.
- Merk celle A1 i regnearket, og trykk CTRL+V.
- Hvis du vil bytte mellom å vise formelen som returnerer resultatet, og resultatet i cellen, merker du cellen og trykker F2 og deretter ENTER, eller klikker Kommandoer og alternativer på verktøylinjen i regnearket, velger kategorien Formel, og ser i boksen Formel i aktiv celle (aktiv celle).
| Formel | Beskrivelse (Resultat) |
|---|---|
| =SINH(1) | Hyperbolsk sinus til 1 (1,175201194) |
| =SINH(-1) | Hyperbolsk sinus til -1 (-1,175201194) |
Eksempel 2
Bruk denne funksjonen når du vil anslå en kumulativ sannsynlighetsfordeling. Sett at en testverdi i et laboratorium varierer mellom 0 og 10 sekunder. En empirisk analyse av resultatene av eksperimenter viser at sannsynligheten for å oppnå et resultat x som er mindre enn t sekunder, kan anslås med følgende ligning:
P(x<t) = 2,868 * SINH(0,0342 * t), der 0<t<10
Hvis du vil beregne hvor stor sannsynligheten er for at resultatet blir mindre enn 1,03 sekunder, setter du inn 1,03 i stedet for t.
Det kan være enklere å forstå eksemplet hvis du kopierer det til et tomt regneark.
- Opprett et tomt regneark.
- Velg eksemplet i hjelpeemnet.

Velg et eksempel fra Hjelp
- Trykk CTRL+C.
- Merk celle A1 i regnearket, og trykk CTRL+V.
- Hvis du vil bytte mellom å vise formelen som returnerer resultatet, og resultatet i cellen, merker du cellen og trykker F2 og deretter ENTER, eller klikker Kommandoer og alternativer på verktøylinjen i regnearket, velger kategorien Formel, og ser i boksen Formel i aktiv celle (aktiv celle).
| Formel | Beskrivelse (Resultat) |
|---|---|
| =2,868*SINH(0,0342*1,03) | Sannsynligheten for å oppnå et resultat på mindre enn 1,03 sekunder (0,101049063) |
Du kan forvente dette resultatet omtrent 101 ganger i løpet av 1000 eksperimenter.
 Hvordan?
Hvordan?