Returnerer skjæringspunktet for den lineære regresjonslinjen som går gjennom datapunkt med kjente x- og y-verdier. Skjæringspunktet er stedet hvor denne regresjonslinjen skjærer y-aksen. Du kan bruke SKJÆRINGSPUNKT når du skal bestemme verdien til den avhengige variabelen når den uavhengige variabelen er lik null. Du kan for eksempel bruke SKJÆRINGSPUNKT til å forutsi et metalls elektriske motstand ved 0°C når datapunktene ble målt ved romtemperatur eller høyere.
Syntaks
SKJÆRINGSPUNKT(kjente_y; kjente_x)
Kjente_y er det avhengige settet observasjoner eller data.
Kjente_x er det uavhengige settet observasjoner eller data.
Kommentarer
- Argumentene må være tall eller navn, matriser eller referanser som inneholder tall.
- Hvis et matrise- eller referanseargument inneholder tall, logiske verdier eller tomme celler, blir disse verdiene utelatt. Celler som inneholder verdien null, tas derimot med.
- Hvis kjente_y og kjente_x inneholder forskjellig antall datapunkt eller ikke inneholder noen datapunkt, returnerer SKJÆRINGSPUNKT feilverdien #I/T!.
- Formelen for skjæringspunktet av regresjonslinjen er:
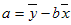
der stigningstallet er beregnet til:
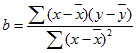
Eksempel
Det kan være enklere å forstå eksemplet hvis det kopieres til et tomt regneark.
- Opprett et tomt regneark.
- Velg eksemplet i hjelpeemnet.

Velg et eksempel fra Hjelp
- Trykk CTRL+C.
- Merk celle A1 i regnearket, og trykk CTRL+V.
- Hvis du vil bytte mellom å vise formelen som returnerer resultatet, og resultatet i cellen, merker du cellen og trykker F2 og deretter ENTER, eller klikker Kommandoer og alternativer på verktøylinjen i regnearket, klikker Formel-kategorien og ser i boksen Formel i aktiv celle (aktiv celle).
| Kjent Y | Kjent X |
|---|---|
| 2 | 6 |
| 3 | 5 |
| 9 | 11 |
| 1 | 7 |
| 8 | 5 |
| Formel | Beskrivelse (resultat) |
| =SKJÆRINGSPUNKT(A2:A6, B2:B6) | Skjæringspunktet for den lineære regresjonslinjen som går gjennom datapunkt med x- og y-verdiene ovenfor. |
 Hvordan?
Hvordan?