Returnerer den individuelle binomiske sannsynlighetsfordelingen. Bruk BINOM.FORDELING ved løsning av problemer med et bestemt antall tester eller forsøk, når utfallet av et forsøk enten er vellykket eller mislykket, når prøvene er uavhengige, og når sannsynligheten for at eksperimentet er vellykket, er konstant gjennom hele eksperimentet. BINOM.FORDELING kan for eksempel brukes til å beregne sannsynligheten for at to av de neste tre fødte barn skal være gutter.
Syntaks
BINOM.FORDELING(antall_s;forsøk;sannsynlighet_s;kumulativ)
Antall_s er antall forsøk med vellykket utfall.
Forsøk er antallet uavhengige forsøk.
Sannsynlighet_s er sannsynligheten for å lykkes ved hvert forsøk.
Kumulativ er en logisk verdi som bestemmer funksjonens form. Hvis kumulativ er lik SANN, returnerer BINOM.FORDELING den kumulative fordelingsfunksjonen, eller sannsynligheten for at det maksimalt er antall_s vellykkede forsøk. Hvis kumulativ er USANN, returneres den sannsynlige mengdefunksjonen for masse, som er sannsynligheten for at det skal bli nøyaktig antall_s vellykkede forsøk.
Kommentarer
- I Antall_s og forsøk strykes eventuelle desimaler, slik at tallene blir heltall.
- Hvis antall_s, forsøk, eller sannsynlighet_s ikke er numeriske verdier, returnerer BINOM.FORDELING feilverdien #VERDI!.
- Hvis antall_s < 0 eller antall_s > forsøk, returnerer BINOM.FORDELING feilverdien #NUM!.
- Hvis sannsynlighet_s < 0 eller sannsynlighet_s > 1, returnerer BINOM.FORDELING feilverdien #NUM!.
- Den binomiske sannsynlighetsfunksjonen for masse er:
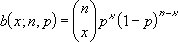
der:

er lik KOMBINASJON(n;x).
Den kumulative binomiske fordelingen er:
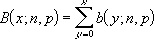
Eksempel
Det kan være enklere å forstå eksemplet hvis det kopieres til et tomt regneark.
- Opprett et tomt regneark.
- Velg eksemplet i hjelpeemnet.

Velg et eksempel fra Hjelp
- Trykk CTRL+C.
- Merk celle A1 i regnearket, og trykk CTRL+V.
- Hvis du vil bytte mellom å vise formelen som returnerer resultatet, og resultatet i cellen, merker du cellen og trykker F2 og deretter ENTER, eller klikker Kommandoer og alternativer på verktøylinjen i regnearket, klikker Formel-kategorien og ser i boksen Formel i aktiv celle (aktiv celle).
| Data | Beskrivelse |
|---|---|
| 6 | Antall vellykkede forsøk i forsøksrekken |
| 10 | Antall uavhengige forsøk |
| 0,5 | Sannsynligheten for å lykkes i hvert forsøk |
| Formel | Beskrivelse (resultat) |
| =BINOM.FORDELING(A2,A3,A4,USANN) | Sannsynligheten for at nøyaktig 6 av 10 forsøk lykkes (0,205078) |
 Hvordan?
Hvordan?